La herramienta Tendencia utiliza una interpolación polinómica global que ajusta una superficie suave definida por una función matemática (polinómica) a los puntos de muestra de entrada. La superficie de tendencia cambia gradualmente y captura patrones de escala sin detallar en los datos.
Fondo conceptual
Conceptualmente, la interpolación por tendencia es como tomar un trozo de papel y ajustarlo entre puntos elevados (a la altura de valor). Esto se demuestra en el siguiente diagrama con un conjunto de puntos de elevación de muestra tomados en una colina con pendiente suave. El trozo de papel está en color magenta.
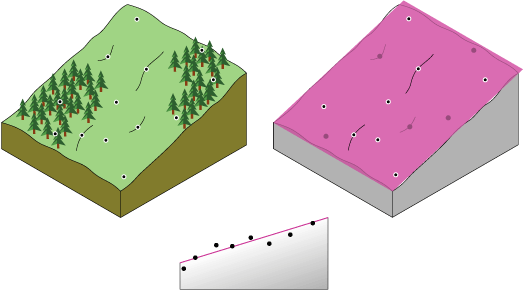
Un trozo de papel plano no capturará de manera precisa un paisaje que contiene un valle. Sin embargo, si dobla el trozo de papel una vez, obtendrá un ajuste mejor. Agregar un término a la fórmula matemática produce un resultado similar, una curvatura en el plano. Un plano chato (sin doblez en el trozo de papel) es una función polinómica de primer orden (lineal). Si se agrega una curvatura es una función polinómica de segundo orden (cuadrática), si se agregan dos curvaturas es de tercer orden (cúbica), y así sucesivamente. Con esta herramienta se permite un máximo de 12 curvas (orden décimo segundo). En la siguiente imagen se muestra conceptualmente una función polinómica de segundo orden ajustada a un valle.
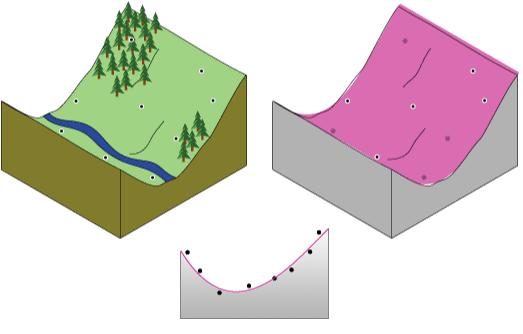
El trozo de papel rara vez pasará por los puntos medidos reales, por lo que la interpolación por tendencia es un interpolador inexacto. Algunos puntos estarán por encima el trozo de papel y otros por debajo. Sin embargo, si suma a qué distancia está cada punto por encima del trozo de papel y a qué distancia está cada punto por debajo del trozo de papel, ambas sumas deberían ser similares. La superficie, en color magenta, se obtiene utilizando un ajuste de regresión por mínimos cuadrados. La superficie resultante minimiza las diferencias cuadradas entre los valores elevados y el trozo de papel.
Cuanto menor sea el error cuadrático medio (RMS), más precisa será la representación de los puntos de entrada en la superficie interpolada. Las funciones polinómicas más comunes son las de primer a tercer orden. La interpolación de superficie de tendencia crea superficies lisas.
Cuándo utilizar la interpolación por tendencia
La interpolación por tendencia produce como resultado una superficie suave que representa las tendencias graduales en la superficie sobre el área de interés. Este tipo de interpolación se puede usar para:
- Ajustar una superficie a los puntos de muestra cuando la superficie varía gradualmente de una región a otra sobre el área de interés, por ejemplo, contaminación sobre un área industrial.
- Examinar o quitar los efectos de las tendencias de largo alcance o globales. En estas circunstancias, la técnica suele denominarse análisis de superficie de tendencia.
La interpolación por tendencia crea una superficie que varía en forma gradual utilizando funciones polinómicas de bajo orden que describen un proceso físico, por ejemplo, contaminación y dirección del viento. Sin embargo, cuanto más compleja sea la función polinómica, más difícil será atribuirle un significado físico. Además, las superficies calculadas son muy susceptibles a los valores atípicos (valores extremadamente altos y bajos), en especial en los bordes.
Tipos de interpolación por tendencia
Hay dos tipos básicos de interpolación por tendencia: lineal y logística.
Tendencia lineal
El interpolador de superficie de tendencia Lineal crea un ráster de punto flotante. Utiliza una regresión polinómica para ajustar una superficie de mínimos cuadrados a los puntos de entrada. Este método permite controlar el orden de la función polinómica utilizada para ajustar la superficie. Para entender este método, piense en una función polinómica de primer orden. Una interpolación de superficie de tendencia lineal de primer orden realiza un ajuste por mínimos cuadrados de un plano al conjunto de puntos de entrada.
La interpolación de superficie de tendencia crea superficies lisas. La superficie generada rara vez pasa por los puntos de datos originales, porque realiza un mejor ajuste para la superficie completa. Cuando se utiliza un orden polinómico mayor que uno, el interpolador puede generar un ráster cuyo mínimo y cuyo máximo superen el mínimo y el máximo del archivo de entrada de los datos de entidad de entrada.
Tendencia logística
La opción Logística para generar una superficie de tendencia es adecuada para obtener una predicción de la presencia o ausencia de ciertos fenómenos (en la forma de probabilidad) para un determinado conjunto de ubicaciones (x,y) en el espacio. El valor z es una variable aleatoria categorizada con sólo dos resultados posibles, por ejemplo, la existencia de una especie en peligro o la inexistencia de esa especie. Estos dos valores z se codifican como uno y cero, respectivamente. Esta opción crea una cuadrícula de probabilidad continua con valores de celda entre uno y cero.
Se utiliza una estimación de posibilidades máxima para calcular el modelo de superficie de probabilidad no lineal sin tener que convertir primero el modelo a la forma lineal.
Archivo RMS de salida
En el archivo de error RMS se guarda el error cuadrático medio de la interpolación comparando el valor de las ubicaciones en el dataset de entrada con el valor de esas mismas ubicaciones en la superficie de ráster interpolada.
El valor del error RMS se puede usar para determinar el mejor valor para usar en el parámetro {order} de la interpolación al cambiar el valor del orden hasta que obtiene el error RMS más bajo. También se registra el valor de chi cuadrado.
Ejemplo
Un ejemplo del archivo RMS de salida desde una ejecución de la herramienta Tendencia con el Orden polinómico fijado en 3 es:
coef # coef
------ ----------------
0 -1192066.7888371
1 -1.78479492586755
2 -0.195982103615487
3 -8.87072249743903e-1
4 -2.0538267625596e-1
5 -3.85610088343239e-1
6 -1.46420255709888e-2
7 -5.31539027745154e-2
8 -2.59261094879031e-3
9 9.71651459136166e-4
------ ----------------
RMS Error = 296.957857221845
Chi-Square = 17019506.0103975El valor predicho en cualquier ubicación del ráster de salida para esta tendencia de tercer orden se puede determinar resumiendo los valores que resultan de una serie de ecuaciones. Para estas ecuaciones, x = la longitud de la ubicación, y = la latitud y el término cn es el valor de coeficiente de la tabla anterior. Las ecuaciones de esta interpolación de tercer orden son:
Prediction(x,y) = c0 +
x·c1 + y·c2 +
x2·c3 + x·y·c4 + y2·c5 +
x3·c6 + x2·y·c7 + x·y2·c8 + y3·c9
Esencialmente, el coeficiente 0 siempre es el de intercepción. Desde ahí, repita los términos de primer orden comenzando con el x más alto y terminando sin ningún x. Continúe con los términos de segundo orden e itere hacia abajo los x de nuevo y haga lo mismo para los términos de tercer orden.
Nota:
Estas ecuaciones siguen un patrón similar a medida que aumenta el orden. Por ejemplo, si se especificó el cuarto orden, habrá cinco valores más especificados en la tabla RMS (coeficientes 10, 11, 12, 13 y 14) y un número acorde de ecuaciones adicionales que los usen.