La herramienta Re-escalar por función le permite usar una función matemática (línea o curva) para asignar valores de adecuación a un ráster de entrada siguiendo una escala continua (normalmente, del 1 al 10). Re-escalar resulta especialmente útil en modelos de adecuación. Muchas veces, la adecuación varía de forma continua al variar los valores del criterio y a menudo lo hace de forma no lineal. Por ejemplo, las ubicaciones de las celdas próximas a carreteras existentes pueden tener la mayor preferencia en un modelo de adecuación para viviendas porque el coste de suministrar electricidad a esas ubicaciones es menor. A medida que la distancia a la carretera aumenta, el coste de suministrar electricidad a esas ubicaciones puede crecer exponencialmente. Como resultado, la adecuación de las localizaciones más alejadas se reduce drásticamente. Una vez que se establece la interacción de costes, el decrecimiento exponencial de la preferencia se transforma en una escala continua de adecuación, por ejemplo una escala del 1 al 10. Entonces es posible integrar el criterio de coste escalado con otro criterio escalado, como la pendiente, la orientación y la distancia hasta los centros educativos para identificar las mejores ubicaciones para viviendas.
Existen cuatro factores principales a tener en cuenta al aplicar esta herramienta:
- Entender y definir la interacción de preferencia entre el fenómeno y el criterio.
- Seleccionar la función de transformación que describa mejor la interacción de la preferencia (por ejemplo, aumento exponencial).
- Opcionalmente, modificar los parámetros de la función para mejorar el ajuste.
- Definir una escala de adecuación (evaluación) para transformar los valores de la función de preferencia (por ejemplo del 1 al 10).
La herramienta Re-escalar por función amplía sus opciones para transformar datos en un modelo de adecuación. Puede utilizar la herramienta Reclasificar para reclasificar datos en categorías, y la herramienta Re-escalar por función para reescalar (reclasificar) datos continuos sin crear categorías discretas. La herramienta Re-escalar por función ofrece una variedad de funciones para crear modelos de adecuaciones que cambian en función de una escala continua. Puesto que la herramienta re-escala los valores del ráster de entrada sobre una escala de adecuación continua, no se produce agregación en categorías, lo cual permite describir mejor interacciones de preferencia que varían de forma continua (por ejemplo la que se describe arriba, en la cual el coste cambia con la distancia respecto de la carretera).
Las funciones disponibles son: Exponencial, Gaussiano, Grande, Lineal, Logaritmo, Decaimiento logístico, Crecimiento logístico, MSLarge, MSSmall, Cercano, Potencia, Pequeño y Lineal simétrico. Puede encontrar más detalles sobre cada una de las funciones aquí:
Es posible definir umbrales inferiores y superiores para controlar mejor cómo se re-escalan los valores de entrada. Consulte Efecto de los umbrales inferior y superior sobre los valores de salida para obtener más detalles.
Vocabulario esencial
Las siguientes definiciones hacen referencia a algunos de los términos más utilizados para describir Re-escalar por función.
- Fenómeno: elemento que se modeliza (por ejemplo, un ciervo, una vivienda, una carretera o un centro comercial).
- Valor de preferencia: valor que indica cuánto prefiere el fenómeno una determinada entidad en una ubicación concreta.
- Criterio: la entidad a la cual responde el fenómeno (por ejemplo, pendiente, orientación, distancia de la carretera o tipo de uso de la tierra).
- Valor de adecuación: coincide con el valor de preferencia, con la salvedad de que la preferencia se produce en el contexto de un modelo de adecuación.
- Escala de evaluación: escala relativa para colocar los valores de preferencia o adecuación. Por lo general, una celda asignada a un valor de evaluación mayor contiene entidades por las cuales el fenómeno tiene mayor preferencia en relación con el criterio que se está analizando. Algunas de las escalas de evaluación frecuentes son del 1 al 10, del 0 al 1 y del 1 al 100.
- Escala de adecuación: lo mismo que la escala de evaluación.
- Valores continuos: valores de un ráster con significado relativo. Por ejemplo, una celda a 100 metros de altura sobre el nivel del mar está a la mitad de altura que una que tenga asignados 200 metros. Ejemplos de datos continuos son la elevación, la concentración de ozono y los valores de adecuación.
- Valores categóricos: valores de un ráster que no tienen significado relativo. Por ejemplo, una celda con un uso del suelo de tipo 4 no es la mitad del uso del suelo de una celda que tiene asignado un tipo 8. Entre los ejemplos de datos categóricos se encuentran el tipo de uso del suelo, nombres de condado y códigos postales.
- Escala de salida continua: valores dentro de un rango que crecen o decrecen de forma continua sin clases discretas. Por lo general, los valores continuos se representan con valores de punto flotante.
Transformación de los datos
La herramienta Re-escalar por función reescala datos continuos sobre una escala de adecuación específica, basada en una función matemática (por ejemplo, Exponencial, Potencia y Logaritmo) que puede seleccionar. Desde el punto de vista conceptual, la transformación de los datos es un proceso en dos pasos, en el que primero se aplica una función de transformación y, a continuación, los valores de la función se representan cartográficamente en una escala de adecuación (normalmente del 1 al 10).
Aplicación de la función de transformación.
La función especificada se aplica a los valores que están dentro de los valores de umbral superior e inferior.
Re-escalado de los datos transformados conforme a la escala de evaluación
El gráfico siguiente ilustra cómo se asignan los valores de la función a la escala de evaluación.
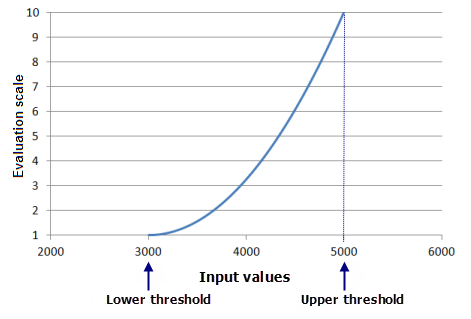
Los valores mínimo y máximo de la función transformada, f(x), se re-escalan al mínimo y el máximo de la escala de evaluación respectivamente. Muchas de las funciones son monótonas (crecen o decrecen continuamente). Como resultado, los umbrales superior e inferior representarán cartográficamente los valores máximo y mínimo en la escala de evaluación por regla general, puesto que serán los valores f(x) más alto y más bajo.
En el ejemplo anterior, los umbrales inferior y superior son iguales al mínimo y el máximo de los datos de entrada (3000 y 5000 respectivamente). Como resultado, al valor de entrada más bajo se le asigna un 1 sobre una escala de evaluación del 1 al 10; al valor de entrada más alto se le asigna un 10. No obstante, este no tiene por qué ser el caso. Por ejemplo, si la función Potencia se aplica a los mismos datos de entrada (entre 3000 y 5000) y, si el umbral inferior está definido en 3500 y el umbral superior en 4500, se le asignará un 1 a una ubicación de celda con valor de entrada de 3500 sobre una escala de evaluación de salida del 1 al 10, y al valor de entrada de 4500 se le asignará un 10. El resto de valores variarán entre los dos en función de su valor transformado. A los valores por debajo del umbral inferior y por encima del umbral superior se les asignarán los valores que se especifiquen.
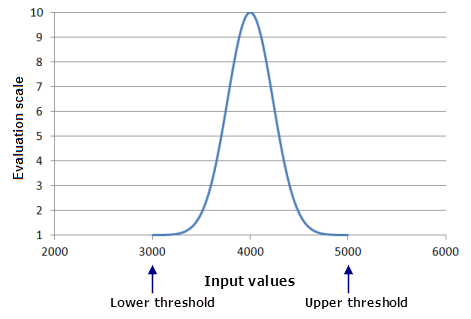
Sin embargo, no todas las funciones crecen o decrecen de forma continua, así que los valores de entrada mínimo y máximo no siempre se corresponden con los valores mínimo y máximo de evaluación. De forma predeterminada, en la función Gaussiano el punto medio es el valor que determina el punto máximo de la función (el valor con la máxima preferencia). Esto corresponde al punto medio de los datos de entrada. Después de aplicar la función Gaussiano, las localizaciones con los valores mínimo y máximo darán lugar a los valores mínimos de la función, f(x). Por este motivo, a las celdas con los valores mínimo y máximo de entrada se les asignará un 1 en el ráster de salida. El valor en el punto medio da lugar al valor máximo de la función, f(x). Como resultado, a las celdas que contengan como valor de entrada este punto medio se les asignará el valor 10 en el ráster de salida.
La función Gaussiano puede ser útil en un modelo de adecuación para identificar el mejor hábitat para una especie rara de orquídeas, la Masdevallia. Esta orquídea es sensible a la elevación. Crece mejor a alturas alrededor de 4.000 metros. A medida que la altura aumenta a partir de ahí, rápidamente resulta demasiado frío para la orquídea. A menores alturas, resulta demasiado cálido. Al re-escalar la elevación, el valor de 4.000 metros es el más preferido y las demás elevaciones (tanto mayores como menores) son las menos preferidas.
Puede asignar cualquier valor de entrada menor que el umbral inferior o mayor que el umbral superior a un valor de salida deseado (dentro o fuera de la escala de evaluación o como NoData) al utilizar los parámetros Valor por debajo del umbral y Valor por encima del umbral. En estas ubicaciones no se aplica la función de transformación.
Definición de la transformación
Existen dos métodos principales a tener en cuenta para definir una transformación continua:
- Acepte los valores predeterminados.
Los parámetros que controlan la forma (véase la descripción más adelante) se calcularán para ajustar la función entre los valores mínimo y máximo del ráster de entrada. Este escenario depende de los datos, puesto que la función se ajusta a los datos.
- Seleccione la función que modelice mejor la adecuación.
Cambie los parámetros de control de la forma de la función hasta lograr la mejor representación posible de la adecuación. Para que la función sea independiente de los datos, establezca los umbrales inferior y superior con valores adecuados para ajustarlos a la preferencia del fenómeno con los valores del criterio independientemente de los valores de los datos de entrada.
Parámetros de la función de transformación
Tipos de parámetros de la función
Existen dos tipos de parámetros asociados a cada función de transformación, los cuales controlan lo siguiente:
- Forma de la función
Algunos ejemplos de estos parámetros son Factor base, Desplazamiento de entrada y Punto medio. Estos parámetros definen la medida en que aumenta o se reduce la función, dónde comienza la evaluación de la función y los puntos de transición dentro de la función.
- Asignación de la función a la escala de evaluación de la adecuación
Algunos ejemplos son los parámetros de umbral, tales como Umbral inferior y Valor por encima del umbral.
Formato general de los parámetros de la función
A continuación se muestra el formato general de los parámetros de cada función y sus características:
- Función ({Parámetro de forma 1}, {Parámetro de forma 2}, {Parámetro de forma 3}, {Umbral inferior}, {Valor por debajo del umbral}, {Umbral superior}, {Valor por encima del umbral})
Para estos parámetros
- Todas las funciones constan de parámetros que controlan la forma y los parámetros de umbral respectivos.
- El número de parámetros de control de forma depende de la función de transformación. La mayoría dispone de dos parámetros, pero algunas utilizan tres.
- Los parámetros de umbral son coherentes entre todas las funciones.
- Los valores predeterminados de los parámetros de control de forma se calculan a partir de valores de datos del ráster de entrada.
- Todos los parámetros de la función son opcionales.
- Los valores de los parámetros Valor por debajo del umbral y Valor por encima del umbral pueden ser un número (doble) o la cadena de caracteres "NoData". Todos los demás parámetros son de tipo doble.
Ejemplo de formato general de la función Exponencial
Para mostrar cómo se aplicaría el formato general descrito anteriormente a una función de transformación concreta, a continuación se muestra cómo serían los parámetros si la función Transformación estuviera definida como Exponencial:
Exponencial (Desplazamiento de entrada, Factor base, Umbral inferior, Valor por debajo del umbral, Umbral superior, Valor por encima del umbral)
Los parámetros Desplazamiento de entrada y Factor base son parámetros de control de la forma. Los parámetros Umbral inferior, Valor por debajo del umbral, Umbral superior y Valor por encima del umbral son parámetros de umbral.
De forma predeterminada, los valores mínimo y máximo de los datos definen los límites inferior y superior de la función.
Interacción de los parámetros en el cuadro de diálogo de la herramienta
En el parámetro Ráster de entrada, el Umbral inferior se ajusta al valor mínimo de ese ráster, el Umbral superior al valor máximo del mismo, y los parámetros de control de forma (por ejemplo, Desplazamiento de entrada, Factor base y Punto medio) se calculan automáticamente para el mejor ajuste (restricción) de la función entre el Umbral inferior y el Umbral superior.
Existe una interacción entre los parámetros de umbral, que controlan la asignación de los valores de la función a la escala de adecuación, y los parámetros de control de forma que definen la curva de la función. Por ejemplo, una vez determinados los valores predeterminados, puede introducir un valor mayor para Umbral superior. Los parámetros de control de la forma asociados se recalcularán y actualizarán en el cuadro de diálogo (por ejemplo, Desplazamiento de entrada y Factor base). No obstante, si escribe un valor nuevo para uno de los parámetros de control de la forma (por ejemplo, un nuevo Factor base), la relación con los parámetros de umbral asociados que controlan la asignación a la escala de adecuación se interrumpe y, por tanto, queda bajo el control del usuario. Utilizando la función Exponencial como ejemplo, si escribe un nuevo Factor base y cambia el Umbral superior, no se recalculará automáticamente otro Factor base. La herramienta utilizará el Factor base que usted especificó. Como segundo ejemplo, esta vez con la función Lineal, de forma predeterminada el valor de Umbral superior es el máximo de Ráster de entrada. Si introduce un valor mayor para el Umbral superior, el parámetro Máximo de la función Lineal se actualizará automáticamente. No obstante, si introduce un nuevo valor para Máximo y cambia el Umbral superior, el parámetro Máximo no cambiará.
Mediante esta interacción en el cuadro de diálogo, la función se ajusta de forma predeterminada entre el Umbral inferior y el Umbral superior, que inicialmente están definidos como el mínimo y el máximo del Ráster de entrada. Sin embargo, es posible controlar totalmente la forma de la función y la asignación a la escala de evaluación introduciendo los valores deseados.
Si cambia un parámetro de una función y desea devolverlo a su valor predeterminado, puede seleccionar y eliminar el valor y, a continuación, hacer clic en el campo de otro parámetro. Esta acción provocará que se vuelva a calcular el valor predeterminado del parámetro que haya dejado en blanco. Por ejemplo, si introduce un valor para Factor base, pero desea que la función vuelva a estar ajustada entre el Umbral inferior y el Umbral superior, elimine el valor del parámetro Factor base y haga clic en el campo de otro parámetro, y se calculará un nuevo Factor base que ajuste la función entre los umbrales.
Nota:
Las funciones MSSmall y MSLarge no siguen este comportamiento de interacción, ya que estas dos funciones dependen del valor medio y la desviación estándar del dataset de entrada.