Disponible con una licencia de Spatial Analyst.

Disponible con una licencia de 3D Analyst.

La herramienta calcula el valor de la derivada segunda de la superficie de entrada celda por celda.

Nota:

La herramienta Curvatura ajusta un plano a las nueve celdas locales, pero un plano puede no ser un buen descriptor del paisaje y puede enmascarar o exagerar variaciones de interés naturales. La herramienta ajusta una superficie a la vecindad de celdas, en lugar de un plano, lo que proporciona un ajuste más natural al terreno.

La herramienta Curvatura utiliza una ventana de celdas de 3 x 3 para calcular el valor, mientras que la herramienta Parámetros de superficie permite tamaños de ventana de 3 por 3 a 15 por 15 celdas. Los tamaños de ventana más grandes son útiles con datos de elevación de alta resolución para capturar procesos de superficie de suelo a una escala adecuada. Parámetros de superficie también proporciona una opción de ventana adaptable, que evalúa la variabilidad local del terreno e identifica el mayor tamaño de vecindad adecuado para cada celda. Puede resultar útil con terreno homogéneo gradual interrumpido por arroyos, carreteras o cortes agudos de pendiente.

La herramienta Parámetros de superficie incluye tres tipos de curvatura, que utilizan fórmulas actualizadas y crean distintos resultados de la herramienta Curvatura.

Para cada celda, una transformación polinómica de cuarto orden de la forma:

Z = Ax²y² + Bx²y + Cxy² + Dx² + Ey² + Fxy + Gx + Hy + I

es adecuada para una superficie compuesta por una ventana de 3 x 3. Los coeficientes a, b, c y sucesivos se calculan desde esta superficie.

A continuación se incluyen relaciones entre los coeficientes y los nueve valores de elevación de las celdas numeradas, como se muestra en el diagrama:

Diagrama de valores de curvatura

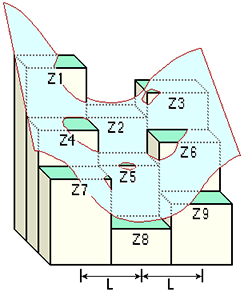
A = [(Z1 + Z3 + Z7 + Z9) / 4 - (Z2 + Z4 + Z6 + Z8) / 2 + Z5] / L4 B = [(Z1 + Z3 - Z7 - Z9) /4 - (Z2 - Z8) /2] / L3 C = [(-Z1 + Z3 - Z7 + Z9) /4 + (Z4 - Z6)] /2] / L3 D = [(Z4 + Z6) /2 - Z5] / L2 E = [(Z2 + Z8) /2 - Z5] / L2 F = (-Z1 + Z3 + Z7 - Z9) / 4L2 G = (-Z4 + Z6) / 2L H = (Z2 - Z8) / 2L I = Z5

La salida de es la suma de las derivadas segundas de la superficie.

Curvatura estándar = -100 * ([d2z/dx2] + [d2z/dy2])

A veces, la curvatura se describe de forma ambigua como la derivada segunda de la superficie, o "pendiente de la pendiente". Esta terminología se refiere a la curvatura de perfil.

Curvatura de perfil = -2(D + E) * 100

Desde un punto de visualización aplicado, la salida de la herramienta se puede utilizar para describir las características físicas de una cuenca de drenaje para intentar entender los procesos de erosión y escorrentía. La pendiente afecta la tasa general de movimiento descendente. La orientación define la dirección del flujo. La curvatura del perfil afecta la aceleración y desaceleración del flujo y, por lo tanto, influye en la erosión y la sedimentación. La curvatura de plano influye en la convergencia y divergencia del flujo.

Interpretar los resultados de la herramienta Curvatura

Mostrar las curvas de nivel sobre un ráster puede ayudar a comprender e interpretar los datos que resultan de ejecutar la herramienta. A continuación, se muestra un ejemplo del proceso con las herramientas identificadas y la configuración utilizada.

1. Cree un ráster de curvatura a partir del ráster de superficie con la herramienta Curvatura:

   Ráster de entrada: elev_ras

   Ráster de curvatura de salida: curv_ras

   Factor z: 1

   Ráster de curvatura de perfil de salida: profile_ras

   Ráster de curvatura plana de salida: plan_ras

2. Cree curvas de nivel del ráster de superficie con la herramienta Curvas de nivel:

   Ráster de entrada: elev_ras

   Entidades de polilíneas de salida: cont_lines

   Intervalo de curvas de nivel: 100

   Curvas de nivel base: ""

   Factor z: 1

3. Cree un ráster de pendiente a partir del ráster de superficie con la herramienta Pendiente:

   Ráster de entrada: elev_ras

   Ráster de salida: slope_ras

   Medición de salida: DEGREE

   Factor z: 1

4. A continuación, cree curvas de nivel del ráster de pendiente con la herramienta Curvas de nivel:

   Ráster de entrada: slope_ras

   Entidades de polilíneas de salida: cont_slope

   Intervalo de curvas de nivel: 5

   Curvas de nivel base: ""

   Factor z: 1

5. Agregue el ráster de curvatura como una capa a la visualización del mapa. Superponga los dos datasets de entidades de curva de nivel recién creados y aplique una simbología de colores diferente para cada uno.

¿Debería utilizar la herramienta Parámetros de superficie?

Si el valor del parámetro Ráster de entrada (in_raster en Python) es de alta resolución con un tamaño de celda inferior a unos pocos metros o especialmente ruidoso, plantéese usar la herramienta Parámetros de superficie y su opción de distancia de vecindad definida por el usuario en lugar de la vecindad 3 por 3 inmediata de esta herramienta. Utilizar una vecindad más grande puede minimizar el efecto de las superficies ruidosas. Utilizar una vecindad más grande también puede representar mejor formas de suelo y características de superficie cuando se utilizan superficies de alta resolución.

Referencias

Moore, I. D., R. B. Grayson y A. R. Landson. 1991. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrological Processes 5: 3–30.

Zeverbergen, L. W. y C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms 12: 47–56.