Cómo funciona Estadísticas de bloque

La herramienta Estadísticas de bloque realiza una operación que calcula una estadística para las celdas de entrada dentro de un conjunto fijo de ventanas o vecindades no superpuestas. La estadística (por ejemplo, valor medio, máximo o suma) se calcula para todas las celdas de entrada contenidas en cada vecindad. El valor resultante para una vecindad o bloque individual se asigna a todas las ubicaciones de celda contenidas en el rectángulo mínimo de delimitación de la vecindad especificada.

Procesamiento de vecindades

Conceptualmente, para cada bloque de celdas, el algoritmo calcula una estadística para las celdas de entrada que quedan dentro de la forma de vecindad especificada en ese bloque. Como las vecindades no se superponen, cualquier celda de entrada específica se incluirá en los cálculos solo para un bloque.

Puede elegir entre varias formas de vecindad predefinidas. También puede crear una forma personalizada. Las estadísticas que puede calcular para una vecindad son: mayoría, máximo, valor medio, mediana, mínimo, minoría, rango, desviación estándar, suma y variedad.

La herramienta Estadísticas de bloque funciona del siguiente modo:

• Crea la primera vecindad especificada (por ejemplo, una vecindad circular) en la esquina superior izquierda de la ventana de análisis.

  

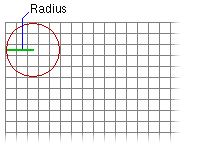
• Calcula el rectángulo mínimo de delimitación para determinar el tamaño del bloque de salida.

  

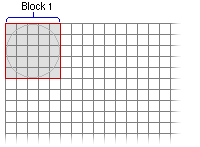
• Divide el área restante del ráster en bloques definidos. Los bloques no se pueden superponer.

  

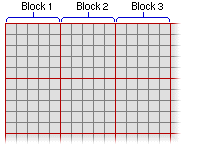
• Identifica las ubicaciones de celda en cada bloque que se utilizarán en los cálculos de bloques. Las ubicaciones de celda se determinan por la definición de la vecindad especificada; por ejemplo, una vecindad circular, que se ajusta al rectángulo de delimitación.

  

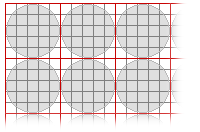
• Calcula el valor de salida para cada vecindad de cada bloque. Los valores resultantes se asignan a cada ubicación de celda en el bloque de salida correspondiente.

Celdas NoData

El parámetro Ignorar los NoData en cálculos controla cómo se procesan las celdas NoData dentro de la ventana de vecindad. Cuando este parámetro está activado (ignore_nodata = "DATA" en Python), cualquier celda de la vecindad que sea NoData se ignora en el cálculo del valor de salida del bloque. Al desactivarla (ignore_nodata = "NODATA" en Python), si cualquier celda de la vecindad es NoData, todas las celdas del bloque de salida serán NoData.

Tamaño de vecindad

El tamaño máximo de cualquier dimensión de vecindad se limita a 2.047 celdas. Esto significa que las vecindades rectangulares no pueden superar este número de celdas en la dirección horizontal o vertical. En el caso de las vecindades circulares, el radio no puede superar las 1.023 celdas.

Tipos de vecindad

La forma de una vecindad puede ser un anillo (donut), un círculo, un rectángulo o una cuña. Con un archivo kernel, también puede definir una forma de vecindad personalizada, además de asignar diferentes pesos a celdas específicas en la vecindad antes de calcular la estadística.

A continuación, se ofrecen descripciones de las formas de vecindad y cómo se definen:

• Anillo
  • La forma de anillo está compuesta por dos círculos, uno dentro del otro, para de esta forma obtener una forma de donut. Las celdas con centros que caen fuera del radio del círculo más pequeño, pero dentro del radio del círculo más grande se incluirán en el procesamiento de la vecindad. El área comprendida entre los dos círculos constituye la vecindad de anillo.
  • El radio se identifica en celdas o unidades de mapa, medidas perpendicularmente al eje x o y. Cuando los radios se especifican en unidades de mapa, se convierten a radios en unidades de celda. Los radios resultantes en unidades de celda generan un área que representa de forma muy fidedigna el área calculada con los radios originales en unidades de mapa. Cualquier centro de celdas que abarca el anillo se incluirá en el procesamiento de la vecindad.
  • La vecindad del anillo predeterminado tiene un radio interno de una celda y un radio externo de tres celdas.
  • La siguiente ilustración de ejemplo muestra una vecindad de anillo:

  

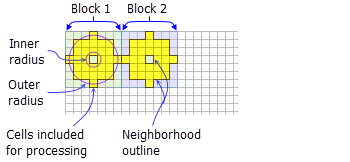
  Se muestran dos bloques de procesamiento con la vecindad de anillo predeterminada (radio interno = 1 celda; radio externo = 3 celdas).

• Círculo
  • Una vecindad de círculo se crea al especificar un valor de radio.
  • El radio se identifica en unidades de celda o de mapa, medidas perpendicularmente al eje x o y. Cuando el radio se especifica en unidades de mapa, se emplea una lógica adicional para determinar qué celdas se incluyen en la vecindad de procesamiento. En primer lugar, se calcula el área exacta de un círculo definido por el valor del radio especificado. A continuación, se calcula el área para dos círculos adicionales, uno con el valor del radio especificado redondeado hacia abajo y otro con dicho valor redondeado hacia arriba. Estas dos áreas se comparan con el resultado del radio especificado, y en la operación se usará el radio del área que esté más cerca.
  • El radio predeterminado de la vecindad de círculo es de tres celdas.
  • La siguiente ilustración de ejemplo muestra una vecindad de círculo:

  

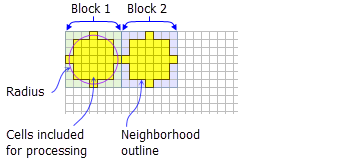
  Se muestran dos bloques de procesamiento con la vecindad de círculo predeterminada (radio = 3 celdas).

• Rectángulo
  • La vecindad rectangular se especifica proporcionando el ancho y la altura en unidades de celda o de mapa.
  • Solo las celdas cuyos centros se encuentren dentro del objeto definido se procesarán como parte de la vecindad rectangular.
  • La vecindad rectangular predeterminada es un cuadrado con un ancho y una altura de tres celdas.
  • La siguiente ilustración de ejemplo muestra una vecindad rectangular:

  

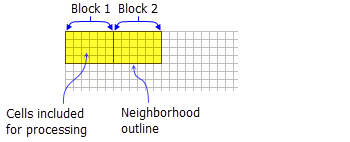
  Se muestran dos bloques de procesamiento con una vecindad de rectángulo (ancho = 6 celdas; altura = 4 celdas).

• Cuña
  • Una cuña es una vecindad con forma de gráfico circular especificada por un radio, un ángulo de inicio y el ángulo de finalización.
  • La cuña se extiende en el sentido contrario a las agujas del reloj desde el ángulo de inicio al ángulo de finalización. Los ángulos se especifican en grados aritméticos de 0 a 360, donde 0 se encuentra en el eje x positivo (las 3:00 en un reloj) y puede ser un entero o un punto flotante. Se pueden utilizar ángulos negativos.
  • El radio se identifica en celdas o unidades de mapa, medidas perpendicularmente al eje x o y. Cuando el radio se especifica en unidades de mapa, se convierte a un radio en unidades de celda. El radio resultante en unidades de celda genera un área que representa de forma muy fidedigna el área calculada con el radio original en unidades de mapa. Cualquier centro de celdas que abarca la cuña se incluirá en el procesamiento de la vecindad.
  • La vecindad en cuña predeterminada es de 0 a 90 grados, con un radio de tres celdas.
  • La siguiente ilustración de ejemplo muestra una vecindad en cuña:

  

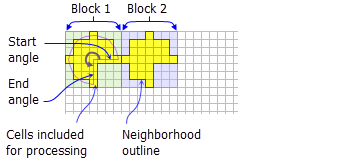
  Se muestran dos bloques de procesamiento con la vecindad de cuña (radio = 3 celdas; ángulo inicial = 0; ángulo final = 270).

• Irregular
  • Le permite especificar una vecindad de forma irregular.
  • El archivo kernel irregular especifica las posiciones de celdas que se deben incluir en la vecindad.
  • Lo siguiente es válido para un archivo kernel de una vecindad irregular:
    • El archivo kernel irregular es un archivo de texto ASCII que define los valores y la forma de una vecindad irregular. El archivo se puede crear con cualquier editor de texto sin formato. Debe tener una extensión de archivo .txt y no contener espacios en el nombre del archivo.
    • La primera línea especifica el ancho y la altura de la vecindad (el número de celdas en la dirección x, seguido de un espacio y el número de celdas en la dirección y).
    • Las líneas subsiguientes definen el valor que se utilizará para cada posición en la vecindad que representan. Se requiere un espacio entre cada valor.
    • Los valores definen si se incluirá en el cálculo una posición en la vecindad. Normalmente, el valor 1 se utiliza para identificar las posiciones a incluir en los cálculos para una vecindad irregular, pero se puede utilizar cualquier valor positivo o negativo que no sea 0. También se pueden utilizar valores de punto flotante.
    • Para excluir del cálculo una ubicación de la vecindad, utilice un valor de 0 (no un espacio en blanco) en la ubicación correspondiente del archivo kernel.

  • El siguiente ejemplo muestra el contenido de un archivo kernel irregular y la vecindad que representa:

  

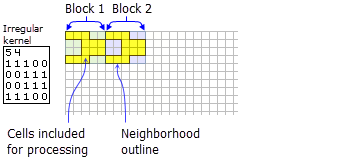
  Se muestra un kernel de vecindad irregular con una ilustración de qué celdas se incluirán en el procesamiento para dos bloques.

• Ponderación
  • De manera similar al tipo de vecindad irregular, la vecindad ponderada permite definir una vecindad irregular, pero además permite aplicar ponderaciones a los valores de entrada.
  • El archivo kernel de peso especifica las posiciones de celda que se deben incluir dentro de la vecindad y las ponderaciones por las que se multiplicarán.
  • La vecindad ponderada solo está disponible para los tipos de estadísticas de valor medio, desviación estándar y suma.
  • Lo siguiente es válido para el archivo kernel de una vecindad ponderada:
    • El archivo kernel de peso es un archivo de texto ASCII que define los valores y la forma de una vecindad ponderada. El archivo se puede crear con cualquier editor de texto sin formato. Debe tener una extensión de archivo .txt y no contener espacios en el nombre del archivo.
    • La primera línea especifica el ancho y la altura de la vecindad (el número de celdas en la dirección x, seguido de un espacio y el número de celdas en la dirección y).
    • Las líneas subsiguientes definen el valor que se utilizará para cada posición en la vecindad que representan. Se requiere un espacio entre cada valor.
    • Para la estadística de suma, un peso puede ser cualquier valor positivo, negativo, entero o de punto flotante.
    • Para las estadísticas de valor medio y desviación estándar, un peso puede ser cualquier valor entero positivo o de punto flotante. No se permiten valores negativos para estas estadísticas, por lo que cualquier posición con un peso negativo se ignorará en los cálculos.
    • Para excluir del cálculo una ubicación de la vecindad, utilice un valor de 0 (no un espacio en blanco) en la ubicación correspondiente del archivo kernel.

  • El siguiente ejemplo muestra el contenido de un archivo kernel de peso y la vecindad que representa:

  

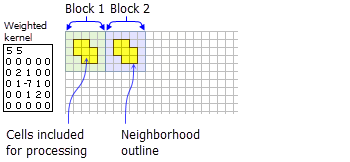
  Se muestra un kernel de vecindad ponderada con una ilustración de las celdas se incluirán en el procesamiento para dos bloques.

Tipo de estadísticas

Las estadísticas disponibles son mayoría, máximo, valor medio, mediana, mínimo, minoría, rango, desviación estándar, suma y variedad. El tipo de estadísticas por defecto es el valor medio.

Algunos tipos de estadísticas solo están disponibles cuando el ráster de entrada es de tipo entero.

• Mayoría
  • Solo se puede utilizar un ráster entero como entrada.
  • Se determina la frecuencia de cada valor de celda único de cada vecindad de bloque. Si existe un solo valor con la frecuencia más elevada (es lo más común), dicho valor se asigna a todas las celdas de esa vecindad. Si hay un empate, se asigna el más bajo de los valores coincidentes.
• Máximo
  • Si el ráster de entrada es un entero, los valores en el ráster de salida serán un entero; si los valores en la entrada son un punto flotante, los valores en la salida serán un punto flotante.
• Valor medio
  • La entrada puede ser de ráster entero o punto flotante.
  • El ráster de salida siempre será un punto flotante.
  • Para el tipo de vecindad ponderada, este es uno de los subconjuntos de tipos de estadísticas que se admiten. Consulte la sección Vecindad ponderada para obtener más información sobre cómo se calcula esta estadística.
• Mediana
  • Solo se puede utilizar un ráster entero como entrada.
  • Si el número de valores de celdas válidos en la vecindad es impar, el valor mediano se calcula a través de la clasificación de los valores y la selección del valor medio. Si el número de valores de una vecindad es par, se clasifican los valores y, de los dos valores centrales, se selecciona el más bajo.
• Mínimo
  • Si el ráster de entrada es un entero, los valores en el ráster de salida serán un entero; si los valores en la entrada son un punto flotante, los valores en la salida serán un punto flotante.
• Minoría
  • Solo se puede utilizar un ráster entero como entrada.
  • Se determina la frecuencia de cada valor de celda único de cada vecindad de bloque. Si existe un solo valor con la frecuencia más baja (es lo menos común), dicho valor se asigna a todas las celdas de esa vecindad. Si hay un empate, se asigna el más bajo de los valores coincidentes.
• Rango
  • Si el ráster de entrada es un entero, los valores en el ráster de salida serán un entero; si los valores en la entrada son un punto flotante, los valores en la salida serán un punto flotante.
  • Los valores para cada ubicación de celda en el ráster de salida se determinan celda por celda al aplicar esta sencilla fórmula: Block Range = Block Maximum – Block Minimum.
• Desviación estándar
  • El ráster de salida siempre será un punto flotante.
  • Para el tipo de vecindad ponderada, este es uno de los subconjuntos de tipos de estadísticas que se admiten. Consulte la sección Vecindad ponderada para obtener más información sobre cómo se calcula esta estadística.
  • La desviación estándar se calcula sobre la población entera (el método N); no se estima sobre la base de una muestra (el método N-1).
• Suma
  • Si el ráster de entrada es un entero, los valores en el ráster de salida serán un entero; si los valores en la entrada son un punto flotante, los valores en la salida serán un punto flotante.
  • Para el tipo de vecindad ponderada, este es uno de los subconjuntos de tipos de estadísticas que se admiten. Consulte la sección Vecindad ponderada para obtener más información sobre cómo se calcula esta estadística.
• Variedad
  • Solo se puede utilizar un ráster entero como entrada.

Cálculos de vecindad ponderada

La cantidad de influencia que tiene cada valor en la vecindad sobre el resultado final del bloque de procesamiento se puede ajustar aplicando ponderaciones.

En las siguientes secciones, se muestran las fórmulas utilizadas para calcular los resultados de las estadísticas de valor medio, desviación estándar y suma ponderados. Un ejemplo acompaña a cada uno mostrando los cálculos para un bloque de procesamiento y los resultados para una vecindad rectangular de 3 x 3 celdas.

Estadística de valor medio ponderado

Para la vecindad ponderada con la estadística de valor medio, el valor de salida de las celdas de un bloque procesamiento es la suma del producto de los valores de peso kernel multiplicada por los valores de entrada, dividido por la suma de los valores de ponderación kernel.

La fórmula aplicada a las celdas dentro de una vecindad es la siguiente:

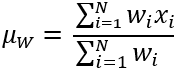
Donde:

• µ_W es el valor medio ponderado de población para el bloque de procesamiento.
• N es el número de celdas de la vecindad.
• w_i es un valor de peso definido en el kernel.
• x_i es un valor de celda de entrada.

Heredado:

En versiones anteriores, los cálculos utilizaban el número de celdas de la vecindad como denominador.

Los valores de peso deben ser valores positivos y pueden ser enteros o de punto flotante.

Ejemplo

Considere el siguiente bloque rectangular de celdas de entrada de 3 x 3:

4 6 7 6 7 8 4 5 6

El promedio matemático (suma / recuento) de estos valores es 53 / 9 = 5,889.

Considere el siguiente kernel de celda ponderado de 3 x 3:

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

Este kernel da el mayor grado de influencia a la celda central del bloque (ponderación de 2), reduce la influencia de los cuatro vecinos ortogonales en la celda central (ponderación de 0,5) y hace que las cuatro celdas de esquina no tengan influencia (ponderación de 0).

Al aplicar la ecuación de valor medio ponderado proporcionada anteriormente, se muestran a continuación los cálculos para lograr el valor final.

=(O1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6 x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w 4 + W5 + w6 + w7 + w8 + w9)= ((0*4)+(0.5*6)+(0*7)+(0.5*6)+(2.0*7)+(0.5*8) +(0*4)+(0.5*5)+(0*6)) / (0+0.5 + 0 + 0.5 + 2.0 + 0.5 + 0) = (0 + 3.0 + 0 + 3.0 + 14.0 + 4.0 + 2.5 + 0) / (0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 14.0 + 14.0 + 4.0 + 2.5) / 4.0 = 26.5 / 4.0 = 6.625

A modo de comparación, el promedio normal de las nueve celdas de entrada sería 5,889. Si solo se incluyen las cinco celdas de entrada que están dentro del kernel (donde el peso != 0) pero sin considerar los valores de los pesos, el promedio sería 6,4 (6 + 6 + 7 + 8 + 5 = 32, que luego se divide por el recuento de cinco).

Estadística de desviación estándar ponderada

Para la vecindad ponderada con la estadística de desviación estándar, el valor de salida de las celdas de un bloque de procesamiento es el resultado de la siguiente ecuación:

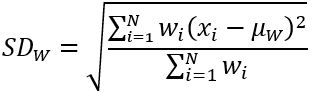
Donde:

• SD_W es el valor de desviación estándar ponderada de población para el bloque de procesamiento.
• µ_W es el valor medio ponderado de población para el bloque de procesamiento.
• N es el número de celdas de la vecindad.
• w_i es un valor de peso definido en el kernel.
• x_i es un valor de celda de entrada.

Los valores de peso deben ser valores positivos y pueden ser enteros o de punto flotante.

Si todos los valores de entrada de una vecindad son iguales, el valor de desviación estándar para todas las celdas de un bloque de procesamiento será 0.

Ejemplo

Los mismos valores de vecindad que se utilizaron en el ejemplo de valor medio ponderado anterior se utilizarán de nuevo para este ejemplo.

4 6 7 6 7 8 4 5 6

También se utilizarán los mismos valores de kernel ponderados:

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

Al aplicar la ecuación de desviación estándar ponderada proporcionada anteriormente para el bloque de celdas, el resultado del cálculo es aproximadamente 0,85696. Este valor se escribirá en cada celda de esta vecindad de bloques.

Estadística de suma ponderada

Para la vecindad ponderada con la estadística de suma, el valor de salida de las celdas de un bloque de procesamiento es el resultado de la siguiente ecuación:

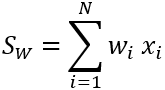
Donde:

• S_W es el valor de suma ponderada para el bloque de procesamiento.
• N es el número de celdas de la vecindad.
• w_i es un valor de peso definido en el kernel.
• x_i es un valor de celda de entrada.

Los valores de peso pueden ser valores positivos o negativos y pueden ser enteros o de punto flotante.

Ejemplo

Considere los siguientes valores de entrada de vecindad:

4 6 7 6 7 8 4 5 6

Considere el siguiente kernel de celda ponderado de 3 x 3:

3 3 -1 -2 -1 0 0 0 1 2 1

Al aplicar la ecuación proporcionada anteriormente, se muestran a continuación los cálculos utilizados para alcanzar el valor final:

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3

Usos para las estadísticas de bloque

Puede utilizar la herramienta Estadísticas de bloque en lugar de la herramienta Remuestrear para remuestrear un ráster de una resolución fina a una menos detallada. En vez de utilizar las técnicas de remuestreo cúbico, bilineal o de vecino más próximo, es posible que sea preferible asignar el máximo, mínimo o promedio de los valores a las celdas de ráster más gruesas en la nueva extensión geográfica que abarcan las celdas más gruesas. Para realizar esto, se aplican las estadísticas adecuadas al bloque; por ejemplo, el promedio (valor medio) o máximo.

La herramienta Agregar del conjunto de herramientas Generalización es similar a Estadísticas de bloque, ya que permite la agregación de ubicaciones de celda basadas en los valores de suma, valor medio, mediana, o mínimo o máximo en una ventana espacial, que se determina según la resolución de salida deseada. Sin embargo, existen dos diferencias principales entre las dos opciones:

• El ráster de salida que resulta de la herramienta Agregar se remuestrea a la resolución deseada.
• No existe el concepto de una vecindad especificada en la herramienta Agregar. La vecindad y el bloque de salida son iguales, siempre rectangulares y abarcan las mismas ubicaciones de celda. El tamaño del bloque en la herramienta Agregar se determina según la agregación de celdas necesarias para alcanzar la resolución deseada.