En la herramienta Re-escalar por función, la función de transformación se aplica a los valores de entrada comprendidos entre (e incluidos) los valores umbral inferior y superior especificados. La definición de los umbrales inferior y superior en relación con los valores de ráster de entrada puede producir resultados muy diferentes. Existen tres casos de uso generales a la hora de especificar los umbrales inferior y superior a los valores de entrada:
- El umbral inferior y superior equivalen a los valores de entrada más bajo y más alto (en función de los datos).
Caso de uso general: determinar la adecuación relativa de las celdas para ciervos dentro de un dataset.
- El umbral inferior es mayor que el valor de entrada más bajo o el umbral superior es menor que el valor de entrada más alto (los umbrales están contenidos en los datos).
Caso de uso general: determinar la adecuación relativa de las celdas para los ciervos dentro de un dataset que contiene valores en los que los ciervos no pueden vivir.
- El umbral inferior es menor que el valor de entrada más bajo o el umbral superior es mayor que el valor de entrada más alto (independiente de los datos).
Caso de uso general: determinar la adecuación relativa de las celdas para ciervos dentro de un dataset en relación con una población mayor de ciervos que viven dentro y fuera del área de estudio.
Escenarios de aplicación de los umbrales inferior y superior
La siguiente tabla resume cinco escenarios para aplicar los tres casos de uso generales anteriores a una función de transformación monótona (crecen o decrecen continuamente) y a una no monótona (varios picos en la función). En los cuatro primeros escenarios se utilizan los valores predeterminados de los parámetros con una escala de evaluación creciente. En el escenario 5 se definen parámetros específicos de control de forma y de umbral.
| Escenario | Efecto |
|---|---|
Monotónica: (La función empleada en el ejemplo es Potencia) | |
1) Los umbrales inferior y superior se definen en el mínimo y el máximo del ráster de entrada. | El valor de entrada mínimo se asigna al valor de Desde escala y el máximo se asigna a la escala Hasta escala, asignándose a todos los demás valores de entrada los valores de evaluación adecuados entre los umbrales. |
2) Los umbrales inferior y superior están dentro del rango de valores del ráster de entrada. | Los valores de entrada correspondientes al Umbral inferior se asignan a Desde escala. Los valores de entrada correspondientes al Umbral superior se asignan a Hasta escala, y a todos los demás valores de entrada se les asignan los valores de evaluación adecuados entre los umbrales. Los valores de entrada inferiores al Umbral inferior se definen como Valor por debajo del umbral, y los valores superiores al Umbral superior se definen como Valor por encima del umbral. |
3) El umbral inferior es menor que el mínimo del ráster de entrada o el umbral superior es mayor que el valor máximo de entrada. | El valor del Umbral inferior se asigna al valor de Desde escala y el Umbral superior se asigna a Hasta escala, asignándose a todos los demás valores los valores de evaluación adecuados entre los umbrales. Como todos los valores de entrada son mayores que el umbral inferior o menores que el umbral superior, es posible que no haya valores de salida que igualen los valores de evaluación de desde y hasta escala en el ráster de salida. |
No monotónica: (La función utilizada en el ejemplo es la gaussiana). | |
4) Los umbrales inferior y superior se definen en el mínimo y el máximo del ráster de entrada. | Los valores de entrada mínimo y máximo se asignan al valor de Desde escala y el punto medio se asigna a Hasta escala, asignándose a todos los demás valores de entrada los valores de evaluación adecuados entre los umbrales. |
5) Los umbrales inferior y superior se definen a un lado de la curva de la función. | Los valores de entrada correspondientes al Umbral inferior se asignan a Hasta escala. Los valores de entrada correspondientes al Umbral superior se asignan a Desde escala, asignándose a todos los demás valores de entrada comprendidos entre los umbrales los valores de evaluación adecuados. Los valores de entrada inferiores al Umbral inferior se definen como Valor por debajo del umbral, y los valores superiores al Umbral superior se definen como Valor por encima del umbral. |
A continuación de la tabla se presenta mediante ejemplos un análisis detallado de cada uno de los cinco escenarios.
Escenario 1
Para definir la función se utilizan los valores predeterminados de la herramienta. Los umbrales superior e inferior se definen en el mínimo y el máximo del dataset de entrada. Como función de ejemplo se utiliza la función Potencia con un exponente de 2 y un desplazamiento de 2999,065.

El rango de valores del ráster de entrada va de 3.000 a 5.000. Todos los valores del ráster se transformarán utilizando la función Potencia. Los valores de la función, f(x), van de 0 a 4.000.000+ (al aplicar el desplazamiento). Este rango de valores de función se re-escala a la escala de evaluación definida de 1 a 10, asignando a la f(x) de 3.000 un 1 en el raster de salida y a la f(x) de 5.000 un 10. En este caso, los valores de entrada mínimo y máximo se asignarán a 1 y 10, respectivamente, en la escala de evaluación de salida.
Situación 2
Los umbrales inferior y superior definidos están dentro del rango de valores del ráster de entrada. Como función de ejemplo se utiliza la función Potencia con un exponente de 2 y un desplazamiento de 3500.

El rango de valores del ráster de entrada va de 3.000 a 5.000. El umbral inferior se fija en 3.500 y el superior en 4.500. El Valor por debajo del umbral se define en 1 y el Valor por encima del umbral se define en 10. La función Potencia se aplica a los valores de entrada comprendidos entre 3.500 y 4.500. El rango de los valores de la función, f(x), (aproximadamente de 0 a 1.000.000) se transforman a la escala de evaluación de 1 a 10. Las celdas con un valor de entrada de 3.500 (el Umbral inferior) se asignarán a 1 y los valores de entrada de 4.500 (el Umbral superior) se asignarán a 10 en la escala de evaluación de salida. Todos los valores comprendidos entre los umbrales se asignarán al valor de la escala de evaluación correspondiente. Observe que los valores mínimo y máximo del ráster de entrada no afectan a los valores de la escala de evaluación de salida. A todas las celdas con un valor de entrada inferior a 3.500 se les asignará 1 y a los valores de entrada superiores a 4.500 se les asignará 10 (los valores definidos para los parámetros por debajo y por encima del umbral); estos valores no se consideran en el rango de valores de la función.
Situación 3
Los umbrales inferior o superior son mayores que el rango de datos de entrada. Como función de ejemplo se utiliza la función Potencia con un exponente de 2 y un desplazamiento de 2000.

El rango de valores del ráster de entrada va de 3.000 a 5.000. El Umbral inferior se fija en 2.000 y el superior en 6.000. La función Potencia se aplicará a los valores comprendidos entre 2.000 y 6.000. Aunque no hay valores de entrada iguales a 2.000 o 6.000, el valor de la función, f(x), para 2.000 y 6.000 se utiliza para definir el rango inferior y superior de f(x). A continuación, el rango de valores de la función se re-escala a la escala de evaluación de 1 a 10. Al valor de la función de 2.000 (el Umbral Inferior) se le asignará un 1, ya que será la f(x) más baja y al valor de la función de 6.000 (el Umbral superior) se le asignará un 10. Sin embargo, como no hay valores de entrada asignados a 2.000 o 6.000, no habrá celdas de salida asignadas a 1 o 10.
Este escenario podría ser útil a la hora de crear un modelo de adecuación del hábitat del ciervo. Es posible que desee que el modelo refleje la preferencia de los ciervos por las ubicaciones dentro del área de estudio en relación con toda la población de ciervos en mayor extensión. En el área de estudio, el valor mínimo para el criterio es de 3.000 y el máximo de 5.000, pero para la extensión mayor que abarca toda la población de ciervos, el valor mínimo es de 2.000 y el máximo de 6.000.
Escenario 4
Los valores de entrada corresponden al umbral inferior y superior (caso predeterminado) de una función que no crece ni decrece continuamente (contiene uno o varios picos). Como función de ejemplo se utiliza la función gaussiana con un punto medio de 4.000 y una dispersión de 0,00000921.

El rango de valores del ráster de entrada va de 3.000 a 5.000. Los umbrales inferior y superior se definen en el mínimo y el máximo del dataset de entrada. La función gaussiana se aplica a los valores de entrada. A continuación, los valores de función resultantes, f(x), se colocan en la escala de evaluación especificada de 1 a 10. Los valores de función de los umbrales inferior y superior son los más bajos de f(x) y se asignan a 1 en la escala de evaluación de la salida. La f(x) del punto medio (4.000) es el valor más alto de la función y, por tanto, se asigna a 10. Tenga en cuenta que, en esta función, los valores del umbral inferior y superior no se corresponden con 1 y 10, respectivamente, en la escala de evaluación.
Escenario 5
El escenario 5 es un caso especial. Como función de ejemplo se utiliza la función gaussiana con un punto medio de 4.000 y una dispersión de 0,00000921 (igual que en el escenario 4).
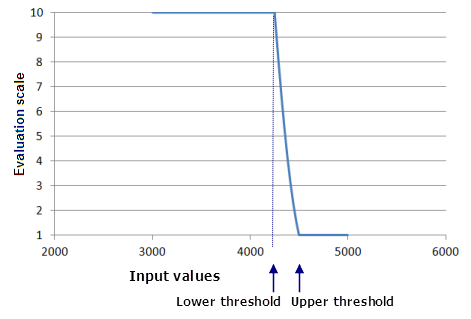
El rango de valores del ráster de entrada va de 3.000 a 5.000. El Valor por debajo del umbral se define en 10 y el Valor por encima del umbral se define en 1. Los umbrales inferior y superior se definen en valores a un lado de la función gaussiana, a 4.250 y 4.500. El punto medio y la dispersión predeterminados, que se establecen en los umbrales alterados, se sobrescriben con los valores especificados (igual que en el escenario 4). Como resultado, la función gaussiana especificada (que no está limitada entre los umbrales) se aplicará solamente a los valores de entrada comprendidos entre 4.250 y 4.500. El rango del valor de la función, f(x), se re-escalará a la escala de evaluación de 1 a 10, asignando el Umbral inferior (valor de entrada 4.250) a 10 en la escala de evaluación y el Umbral superior (valor de entrada 4.500) a 1.