Un índice es un número que mide un tema de interés, a menudo algo difícil de medir o definir directamente, como la vulnerabilidad social o la innovación empresarial. La herramienta Calcular índice compuesto crea un índice combinando varias variables en una sola variable. La herramienta sigue un flujo de trabajo de tres pasos para preprocesar las variables, combinarlas y postprocesar el índice.
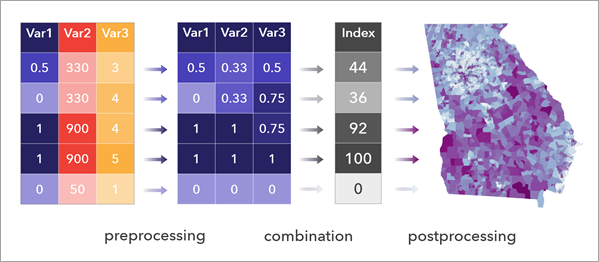
La construcción adecuada de un índice se basa en la profunda consideración de su propósito durante el diseño y la transparencia del proceso durante la comunicación. La herramienta Calcular índice compuesto le guía a través del proceso de creación de un índice adecuado y le ayuda a visualizar y comprender los resultados.
Más información sobre las prácticas recomendadas para crear índices compuestos en ArcGIS
Potenciales aplicaciones
A continuación, se indican las aplicaciones potenciales de la herramienta Calcular índice compuesto:
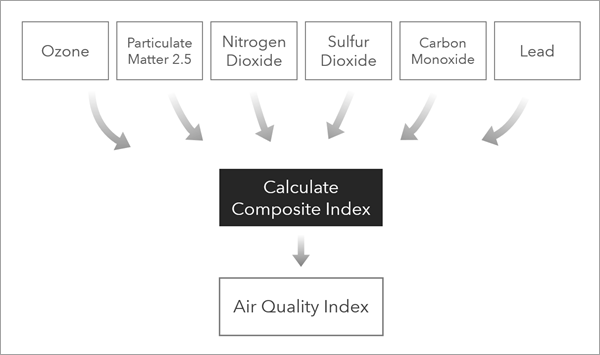
- Un departamento de protección medioambiental desea crear un índice de calidad del aire como información para las políticas públicas y para la población sobre la contaminación. Recopilan datos de estaciones de monitoreo correspondientes a los contaminantes que cumplen los criterios. Un analista puede ejecutar la herramienta Calcular índice compuesto para combinar los indicadores individuales de contaminantes en un único índice de calidad del aire.
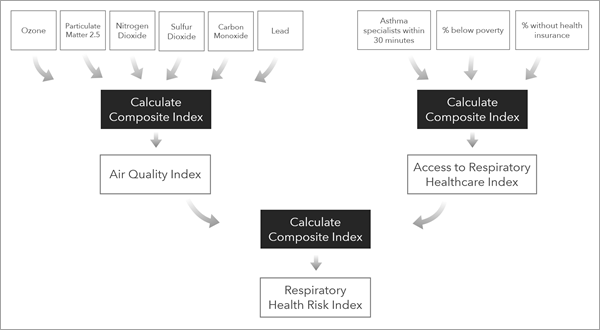
- Un departamento de salud pública desea crear un índice de riesgo de salud respiratoria para destacar las injusticias ambientales. Para ello, el analista puede ejecutar la herramienta Calcular índice compuesto varias veces para crear un índice con varios subíndices, en los que la primera ejecución de la herramienta crea subíndices para diferentes dominios y la última ejecución de la herramienta crea el índice final.
- Una jurisdicción quiere solicitar una subvención de infraestructuras, y para optar a ella necesitan demostrar que los recursos se destinarán a comunidades con servicios insuficientes. Pueden crear un índice que combina variables demográficas y de infraestructura para identificar las áreas con menos servicios.
Cómo se procesan previamente las variables
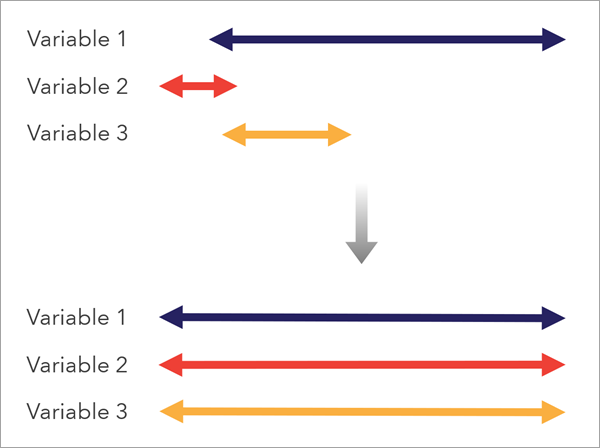
Para crear un índice adecuado, las variables deben estar en una escala compatible. Para lograrlo, se ofrecen opciones de preprocesamiento en la herramienta que aportan distintas variables de entrada a una escala de medición común para que se puedan combinar adecuadamente. Opcionalmente, la herramienta también invierte las variables de manera que el significado de los valores altos en cada variable se alinee entre sí.
Nota:
Utilice la herramienta Transformar campo para transformar variables.
Preprocesar variables para invertir la dirección
Tenga en cuenta el significado de los valores bajos y altos de cada variable y asegúrese de que sean coherentes entre sí. Por ejemplo, en un índice de vulnerabilidad social, las ubicaciones con ingresos medios más bajos son más vulnerables, pero las ubicaciones con porcentajes bajos de personas sin seguro son menos vulnerables; la dirección de estas variables se opone en el contexto de la finalidad del índice.
A medida que introduce cada variable en la herramienta, plantéese si la variable se debe invertir; en cuyo caso, active la casilla de verificación Invertir dirección para invertir la dirección de la variable.
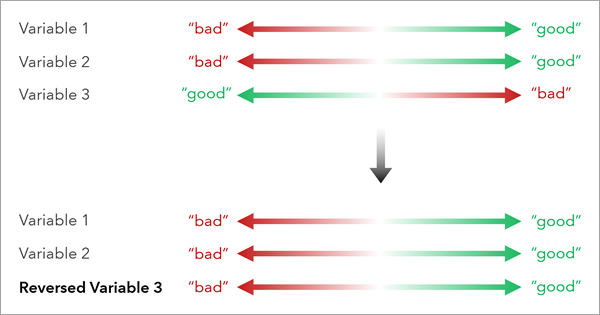
La inversión de la variable se calcula multiplicando cada valor por -1 y escalando el campo entre el rango original de la variable.
Preprocesar variables para utilizar la misma escala
Utilice el parámetro Método para escalar variables de entrada para seleccionar un método de escala común. El método seleccionado se aplicará a todas las variables y los campos resultantes se proporcionan en la salida. Las siguientes opciones están disponibles:
Mínimo-máximo: este método escala las variables entre 0 y 1 utilizando los valores mínimo y máximo de cada variable. Este método es el más sencillo, ya que conserva la distribución de las variables de entrada y las escala a una escala de 0 a 1 que sea fácil de interpretar.
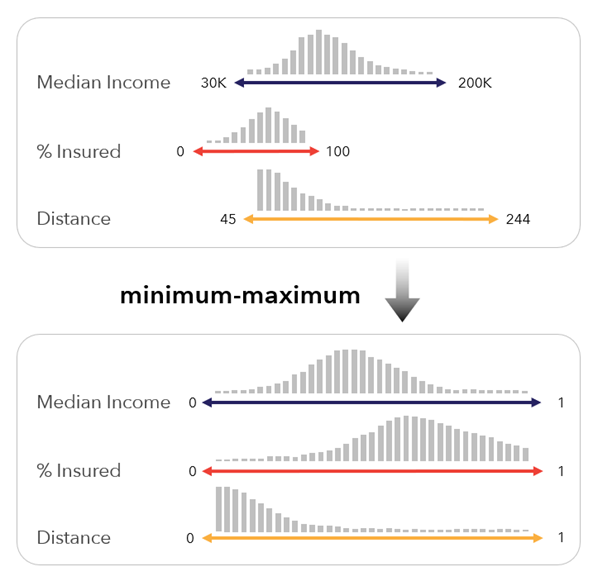
Este método aplica la siguiente fórmula:
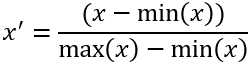
Dado que este método conserva la distribución de variables, puede verse afectado por valores atípicos y distribuciones sesgadas. Por ejemplo, si hay un único valor atípico con un valor muy alto, el valor atípico recibirá un valor de 1, pero el resto de los valores serán similares y más cercanos a cero. Como consecuencia de la variación reducida en la variable preprocesada, esta variable puede tener menos influencia en el índice resultante.
Este método también depende de los valores mínimo y máximo de los datos de entrada, lo que hace que sea menos adecuado para comparaciones de índice en varios periodos de tiempo, cuando los valores mínimo y máximo de una variable pueden cambiar con cada periodo de tiempo.
Mínimo-máximo (rangos de datos personalizados): este método escala las variables entre 0 y 1 mediante los valores mínimos posibles y máximos posibles para cada variable. Este método es útil cuando el mínimo y el máximo posibles no existen en el rango de la variable o si desea crear un índice que deba seguir siendo comparable a medida que se recopilan datos adicionales.
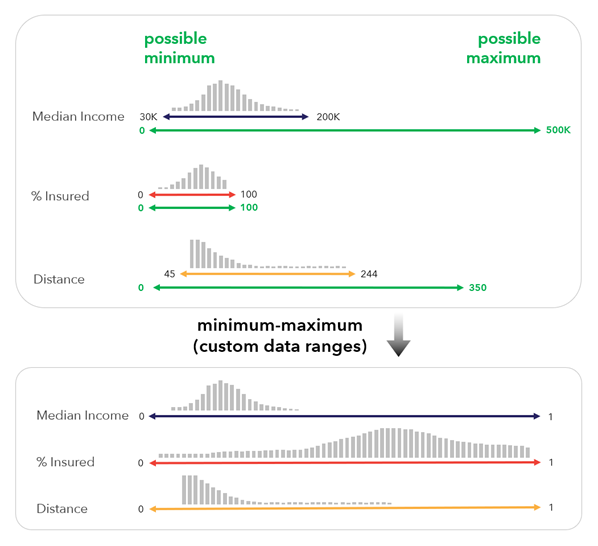
Este método aplica la siguiente fórmula:
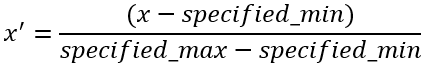
Existen varios casos de uso para establecer un mínimo posible y un máximo posible:
- Cuando el índice se va a comparar a lo largo del tiempo y los datos actuales no representan el rango de valores que el índice podría tener en otros períodos de tiempo.
- Cuando hay una estadística de referencia, como el mínimo y el máximo de un área de estudio más amplia. Por ejemplo, un índice con un área de estudio establecida en Francia puede utilizar un mínimo y máximo basado en todos los países de Europa.
- Cuando hay un punto de referencia al que se aspira, como la esperanza de vida a la que se aspira en un índice de desarrollo humano. Si bien es posible que los datos en sí no tengan la esperanza de vida a la que se aspira, el punto de referencia aún se utiliza para definir contexto para el índice.
- Cuando hay un conocimiento a priori de los valores mínimo y máximo teóricos para variables, como conocer los rangos de temperatura absoluta en la Tierra y utilizar registros diarios con un rango más pequeño.
Percentil: este método convierte las variables a percentiles entre 0 y 1. Este método puede ser útil cuando las clasificaciones de cada variable son más importantes que sus valores reales. También es sólido para los valores atípicos y las distribuciones sesgadas, ya que las variables se transforman en una distribución uniforme.
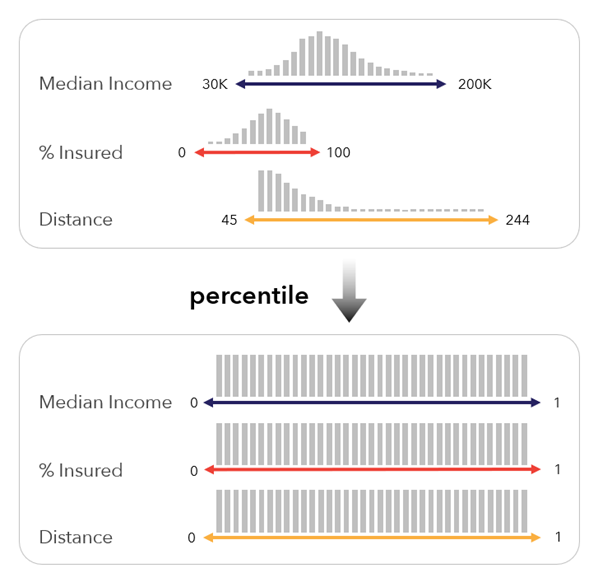
Hay varias definiciones para los percentiles. Este método utiliza la siguiente fórmula:
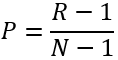 ,
,donde R es la clasificación ordinal (con el valor de clasificación mínimo en el caso de empates), N es el número de valores y P es el percentil resultante.
Los percentiles indican la posición de un valor en relación con el resto de valores de la variable. Por ejemplo, aunque la diferencia de ingresos entre 50.000 y 60.000 dólares puede no ser sustancial, la diferencia de percentil puede ser considerable si hay muchas entidades con valores intermedios.
Clasificación: este método clasifica los valores de entrada, asignando un valor de 1 al valor más bajo de la variable e incrementando en 1 a cada valor. Este método puede ser útil cuando las clasificaciones de cada variable son más importantes que sus valores reales. El método también es sólido para los valores atípicos y las distribuciones sesgadas.
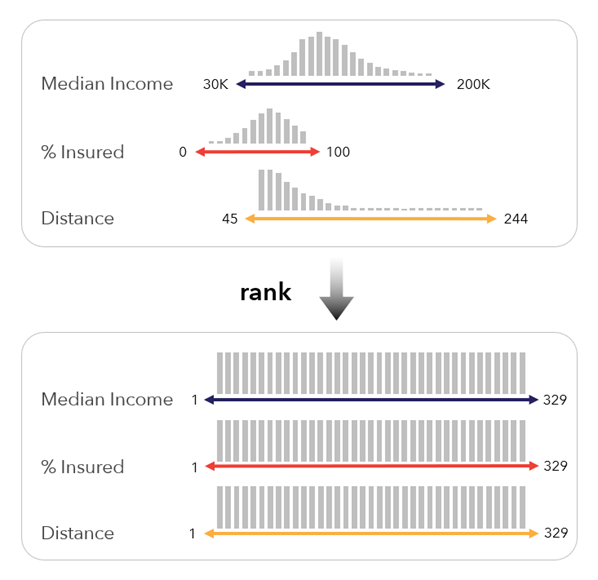
El método utiliza el método de promedio de clasificación, que resuelve los empates asignando el valor de clasificación medio a las observaciones empatadas.
Este método es muy similar a los percentiles, pero el rango de los valores está entre 1 y el número de registros de la tabla.
Puntuación z: este método estandariza cada variable con la fórmula de puntuación z. Este método es útil cuando se debe considerar cada valor con respecto al valor medio de la variable. Por ejemplo, cuando desea saber si el porcentaje de personas por debajo del umbral de la pobreza es mayor o menor que la media nacional y por cuánto.
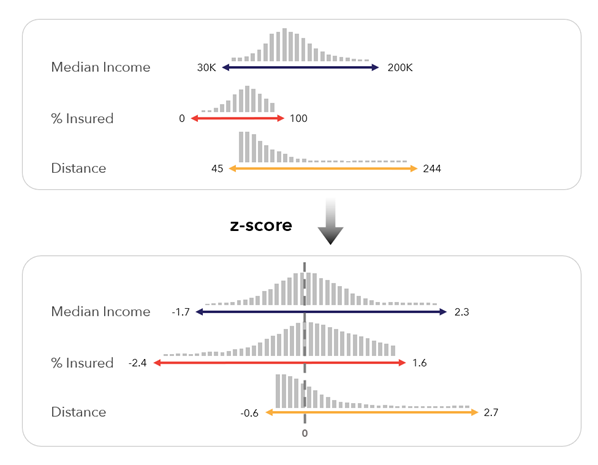
Este método utiliza la siguiente fórmula:
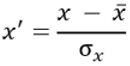 ,
,donde x' es la puntuación z, x es el valor original, x̄ es el valor medio (promedio) y σ es la desviación estándar.
Las puntuaciones z se expresan en desviaciones estándar, una medida de dispersión en los datos. Una puntuación z de 2 significa que la entidad es dos desviaciones estándar mayor que el valor medio, y una puntuación z de -1 es una desviación estándar menor que el valor medio. El método es menos susceptible a los efectos adversos de los valores atípicos cuando se compara con el método mínimo-máximo. Sin embargo, produce valores negativos, por lo que es incompatible con los métodos de combinación multiplicativa.
Puntuación z (personalizada): este método estandariza cada variable utilizando la fórmula de puntuación z con un valor medio personalizado y una desviación estándar personalizada. Este método es útil cuando se crean índices que se comparan con una estadística de referencia o se comparan a lo largo del tiempo.
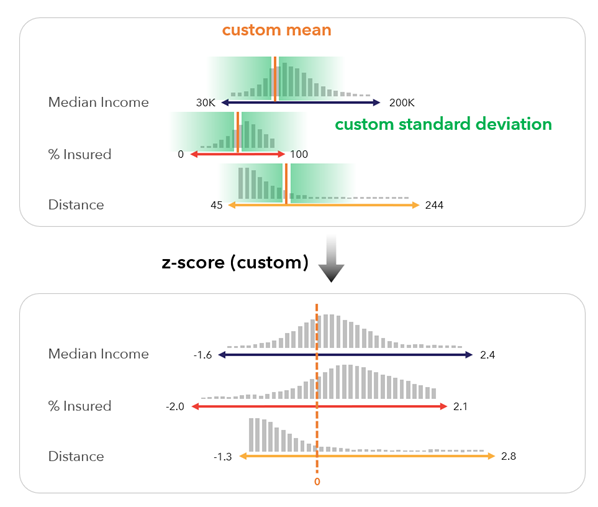
Este método utiliza la siguiente fórmula:
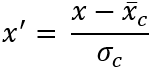 ,
,donde x' es el valor estandarizado, x es el valor original, x̄c es el valor medio personalizado y σc es la desviación estándar personalizada.
Utilice el parámetro Estandarización personalizada para establecer el valor medio de referencia y la desviación estándar.
Por ejemplo, para crear un índice de desarrollo anual que se actualizará en los próximos 10 años utilizando el primer año como punto de comparación, cree un índice para el primer año mediante la opción puntuación z que utilice el valor medio y la desviación estándar reales para cada variable. A continuación, utilice el mismo valor medio y desviación estándar en el parámetro Estandarización personalizada en los años posteriores. De este modo, los resultados se pueden comparar a lo largo de todos los años utilizando la distribución del primer año como comparación.
Este método también es útil al comparar valores con un valor medio teórico que puede no ser igual al valor medio de los datos. Por ejemplo, si la tasa de desempleo nacional es del 8 por ciento, pero la tasa de desempleo promedio de los datos es del 13 por ciento, las puntuaciones z se pueden establecer en relación con una media nacional y una desviación estándar nacional, y la muestra de los datos tendrá más valores positivos para reflejar que la tasa de desempleo es mayor que una media nacional.
Marcar por umbral (binario): este método convierte la variable en valores binarios (0, 1) que indican si el valor está por encima o por debajo de un umbral especificado. Este método es útil cuando es importante resaltar ciertos valores y la variación de los valores no importa.
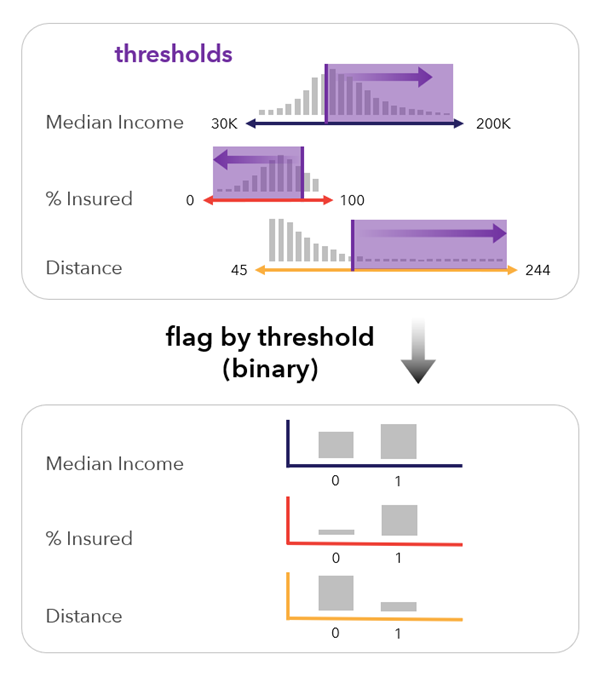
Esta opción activa el parámetro Método para escalar para umbrales, que permite establecer los umbrales en el rango de una variable escalada.
Hay una variedad de casos de uso para este método:
- Los expertos del ámbito de la calidad del aire desean resaltar las ubicaciones donde se supera el umbral saludable para humanos para varias variables de calidad del aire. Establecen las variables del parámetro Método para escalar para umbrales como sin procesar y especifican los umbrales.
- Una agencia gubernamental desea resaltar las ubicaciones que son muy vulnerables en varios dominios. Establecen el parámetro Método para escalar para umbrales como percentil y establecen el umbral en Mayor que 0,9 para que cada variable resalte las ubicaciones más desfavorecidas.
- Una organización internacional desea resaltar países que están sistemáticamente por debajo de la media de los indicadores de desarrollo humano. Establecen el parámetro Método para escalar para umbrales como puntuación z y establecen los umbrales en Menor que 0 para identificar ubicaciones por debajo del valor medio.
Este método es más útil cuando se combina con la opción de combinación de suma para contar el número de veces que una ubicación excede los umbrales.
El método no se ve afectado por los valores atípicos de las variables de entrada, pero se pierde la información del nivel de intervalo de cada variable de entrada, ya que cada variable se convierte en un formato binario (0, 1).
Valores sin procesar: utiliza los valores originales de la variable.
Este método solo se debe utilizar si todas las variables están en una escala comparable. Por ejemplo, cuando todas las variables son una unidad estándar, como porcentajes o partes por millón. Este método también puede ser útil cuando la estandarización o transformación de variables ya se ha producido antes de ejecutar la herramienta.
Nota:
La opción de escalado seleccionada se aplica a todas las variables. Cuando necesite aplicar diferentes opciones de escalado a cada variable, utilice otras herramientas como Estandarizar campo o Reclasificar campo antes de utilizar esta herramienta.
Si un campo tiene valores nulos, la herramienta no podrá calcular ningún índice para los registros. Plantéese utilizar la herramienta Rellenar valores que faltan para imputar un valor, si procede, o buscar datos complementarios de lo contrario.
Cómo la herramienta combina variables en un índice
Una vez que las variables se preprocesan a una escala común, las variables se agregan para crear un valor único. El parámetro Método para combinar variables escaladas tiene las siguientes opciones:
- Suma
- Valor medio
- Multiplicar
- Valor medio geométrico
Las opciones Suma y Valor medio se consideran métodos aditivos, y las opciones Multiplicación y Valor medio geométrico se consideran métodos multiplicativos.
Métodos aditivos
Los métodos de combinación Suma y Valor medio son relativamente sencillos de interpretar y los suelen utilizar una variedad de índices. Los métodos son casi idénticos; dan como resultado distribuciones con la misma forma que solo difieren en escala y, por lo tanto, el mapa de índice resultante tendrá el mismo aspecto. Solo los valores difieren.
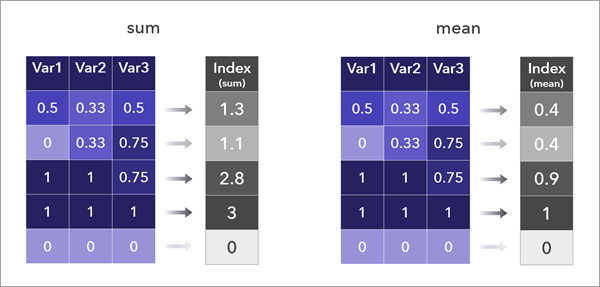
Estos métodos permiten que los valores altos de una variable compensen los valores bajos de otra variable.
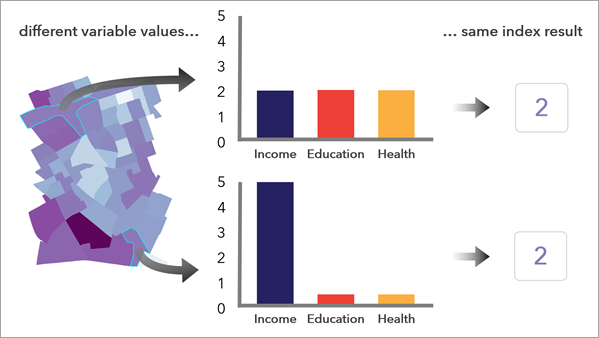
Métodos multiplicativos
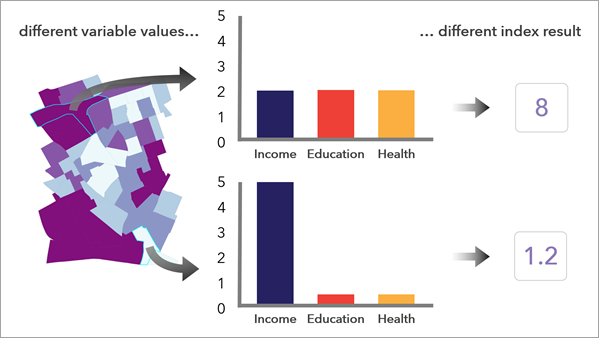
Los métodos Multiplicación y Valor medio geométrico requieren más precaución en su uso, ya que los valores de índice resultantes pueden ser mucho más altos que cuando se utiliza un método aditivo y los métodos no funcionan bien cuando se utilizan valores negativos.
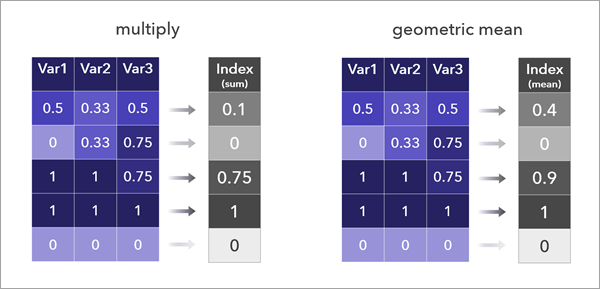
A pesar de sus desventajas, los métodos multiplicativos tienen la ventaja de no permitir que los valores altos de una variable compensen los valores bajos de otra variable; para que un valor de índice sea alto, varias variables deben tener valores altos.
Nota:
El parámetro Método predefinido para escalar y combinar variables proporciona plantillas que definen los métodos de preprocesamiento y combinación basados en enfoques de uso común para crear índices.
Ponderación
Las variables se pueden ponderar para representar la importancia relativa de cada factor a medida que contribuye al índice. De forma predeterminada, todas las ponderaciones se establecen en 1, lo que significa que cada variable se pondera igual. Sin embargo, puede ser importante indicar las diferencias en las contribuciones relativas de una variable en comparación con las demás. Al cambiar una de las variables a una ponderación de 2 y mantener a las demás en 1, se indica que la variable se debe considerar dos veces más importante que las demás en su contribución al índice final.
También puede utilizar ponderaciones que sumen hasta 1; por ejemplo, si se utilizan tres variables y una se debe considerar el doble de importante que las otras dos, puede utilizar valores de ponderación de 0,5, 0,25 y 0,25.
En los métodos aditivos, las ponderaciones se aplican multiplicando cada variable por su peso correspondiente. En los métodos multiplicativos, las ponderaciones se aplican elevando cada variable a la potencia de su peso correspondiente.
Los pesos tienen un impacto significativo en el índice resultante. Tanto si elige mantener las ponderaciones iguales como si desea modificarlas para favorecer las variables, el uso de ponderaciones agrega subjetividad al análisis. Además, puede ponderar involuntariamente debido a la correlación y las diferencias en la varianza entre las variables. Para obtener más información sobre el impacto de la correlación y la varianza en el índice, consulte el documento de prácticas recomendadas para crear índices compuestos.
Cómo se posprocesa el índice
Una vez que las variables se han preprocesado y combinado en el índice sin procesar, el procesamiento posterior puede ayudar a que el índice sea más comprensible. Las opciones de la categoría de parámetro Configuración de salida le permiten ajustar la dirección, ajustar la escala y clasificar los valores.
Invertir el índice
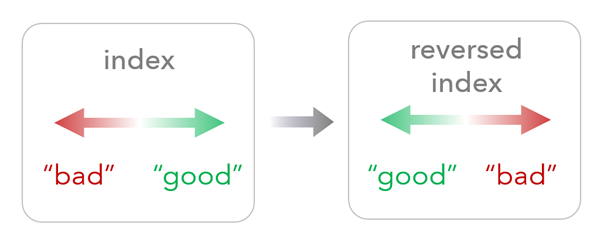
Considere la finalidad del índice y evalúe si los valores altos del índice son los previstos. Utilice la casilla de verificación del parámetro Invertir valores de índice de salida para invertir opcionalmente el índice sin procesar para que los valores altos se conviertan en valores bajos y viceversa.
Nota:
La inversión de los valores de índice para métodos multiplicativos debe realizarse con precaución, ya que estos resultados diferirán de la inversión de las variables de entrada.
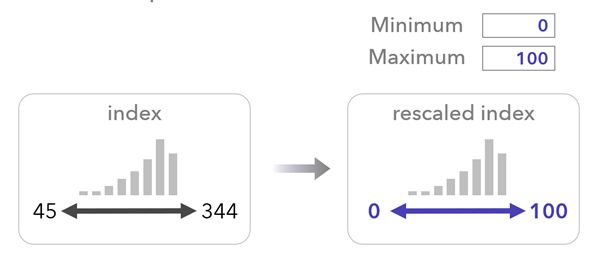
Escalar el índice utilizando los valores mínimo y máximo
Utilice el parámetro Valores mínimo y máximo del índice de salida para especificar el rango del índice de salida. Esta opción puede ser útil para utilizar una escala que pueda ser más fácil de interpretar, independientemente de los métodos de preprocesamiento y combinación seleccionados. Por ejemplo, especifique un valor Mínimo de 0 y un valor Máximo de 100 para escalar el índice sin procesar a este rango. La opción utiliza la siguiente fórmula:
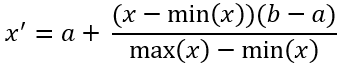 ,
,
donde x es el valor original, min(x) es el valor mínimo encontrado en el índice, max(x) es el valor máximo encontrado en el índice, a es el valor mínimo especificado, b es el valor máximo especificado y x' es el valor escalado.
Clasificar el índice
Además de la salida del índice sin procesar, puede clasificar opcionalmente el índice de salida para ayudarle a interrogar los resultados. El parámetro Salidas clasificadas adicionales tiene cuatro métodos que se pueden utilizar: Intervalo equivalente, Cuantil, Desviación estándar y Personalizado, cada uno de los cuales da lugar a un campo adicional en la salida.
El método de intervalos equivalentes divide el rango del índice en intervalos de igual longitud.
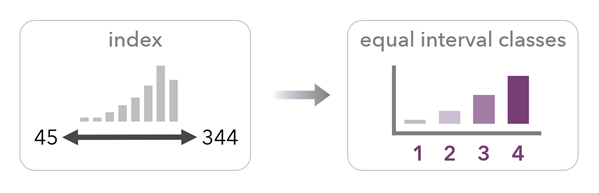
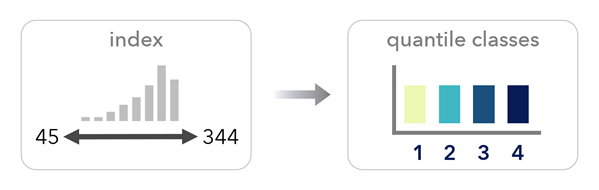
El método de cuantil divide los valores en clases para que cada clase tenga el mismo número de entidades o filas. Este método produce un mapa similar a la capa de percentil del índice, pero utiliza clases, a diferencia de la distribución de percentil continua. Utilice esta opción para crear un mapa de quintiles (con cinco clases), deciles (con 10 clases) u otros tipos de cuantiles basados en el número de clases.
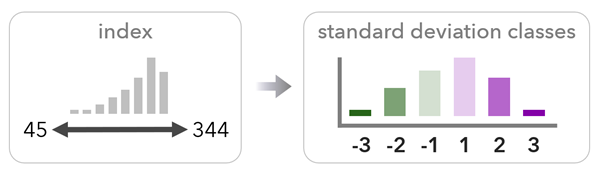
El método de desviación estándar clasifica el índice para mostrar el número de desviaciones estándar a las que se encuentra cada valor del valor medio.
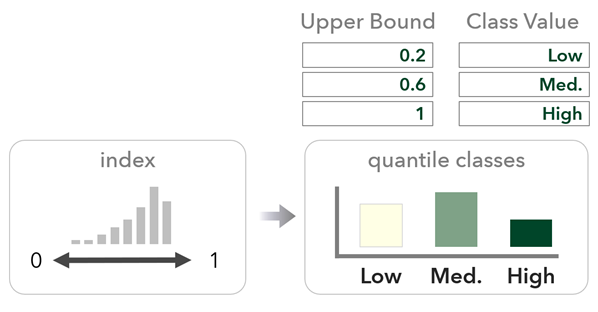
El método de clases personalizadas categoriza el índice continuo mediante límites de clase personalizados y etiquetas personalizadas. Puede agregar etiquetas numéricas o de texto, como Bajo, Medio y Alto.
Interpretar los resultados
Visualizar e investigar el índice resultante es un paso importante para preparar el índice para su uso posterior. La herramienta produce varios mapas y gráficos para ayudarle a interpretar el resultado.
Capas de salida
Cuando el parámetro Entidades o tabla de salida se establece en una clase de entidad o shapefile (en lugar de incorporarlo a la entrada), la herramienta crea varias capas que se incluyen en la capa de grupo de salida:
Sugerencia:
Utilice los accesos directos Ctrl y Mayús para visualizar o contraer rápidamente las capas de la capa de grupo.
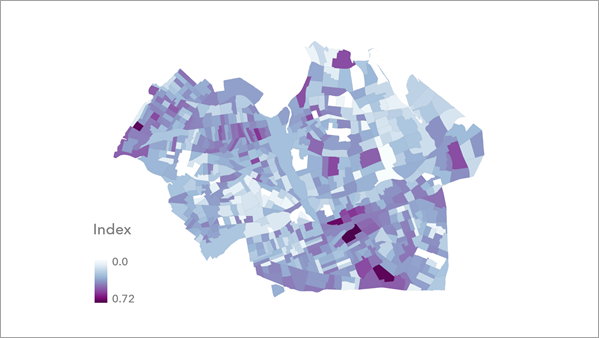
La capa de índice muestra la distribución de los valores de índice después de cualquier escalado o inversión opcional. La capa proporciona un mapa de coropletas continuo que se puede utilizar para evaluar los resultados del índice. Puede utilizar el mapa para evaluar valores de índice altos y bajos y conservar la distribución del índice y cualquier valor atípico.
La capa de percentil del índice muestra las posiciones relativas (clasificaciones) entre los valores de índice. Los colores de mapa resultantes corresponden a las clasificaciones de los valores de índice, de modo que no conservan la distribución ni ninguna diferencia de índice real. Utilice este método cuando desee evaluar cómo se relacionan las ubicaciones entre sí en función de su clasificación de índice.

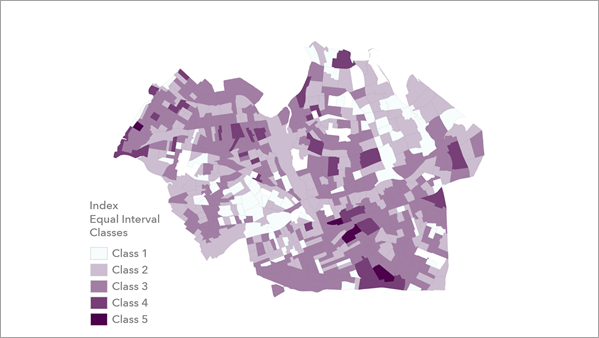
La capa de clases de intervalos equivalentes del índice muestra las clases en función de la distribución de valores del índice, pero agrupa los valores en clases en función de los intervalos equivalentes establecidos en el parámetro Número de clases del índice de salida. Esta capa es una forma clasificada de la capa de índice.
La capa de cuantiles del índice asigna el mismo número de entidades a cada clase y es una forma clasificada de la capa de percentil del índice. El número de clases se establece en el parámetro Número de clases del índice de salida.

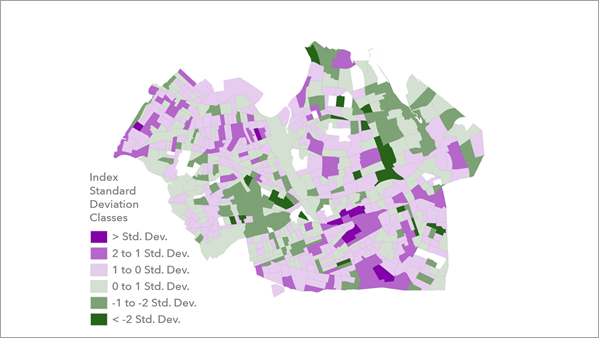
La capa de clases de desviación estándar del índice visualiza ubicaciones por encima y por debajo del valor medio del índice. El esquema de color ayuda a resaltar valores de índice extremadamente altos y bajos, lo que puede resultar útil para identificar las ubicaciones que pueden necesitar más investigación.
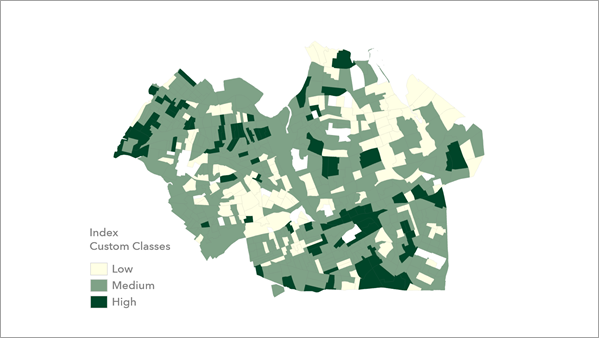
La capa de clases personalizadas del índice muestra las categorías especificadas en el mapa y se puede utilizar para muchos fines, como dividir un índice continuo en categorías desiguales en función de las intervenciones previstas. Por ejemplo, puede llamar a las clases Bajo, Medio y Alto.
Gráficos de salida
La herramienta produce gráficos que se pueden utilizar para ayudar a responder varias preguntas sobre el índice.
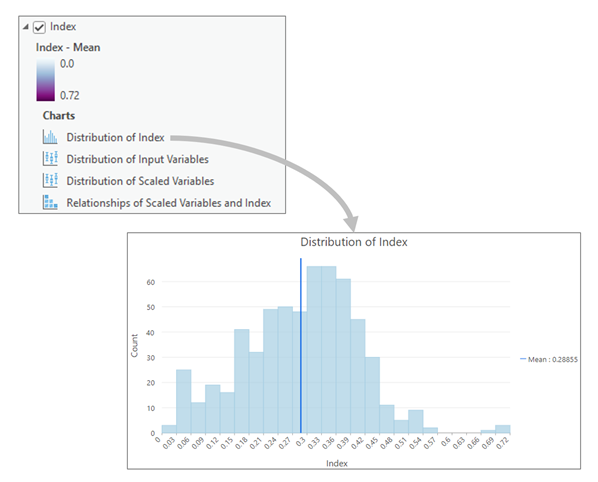
Explorar la distribución del índice
La capa de índice principal de la salida de la capa de grupo contiene un histograma de la distribución del índice. Junto con el mapa, puede ayudarle a comprender la distribución de los resultados.
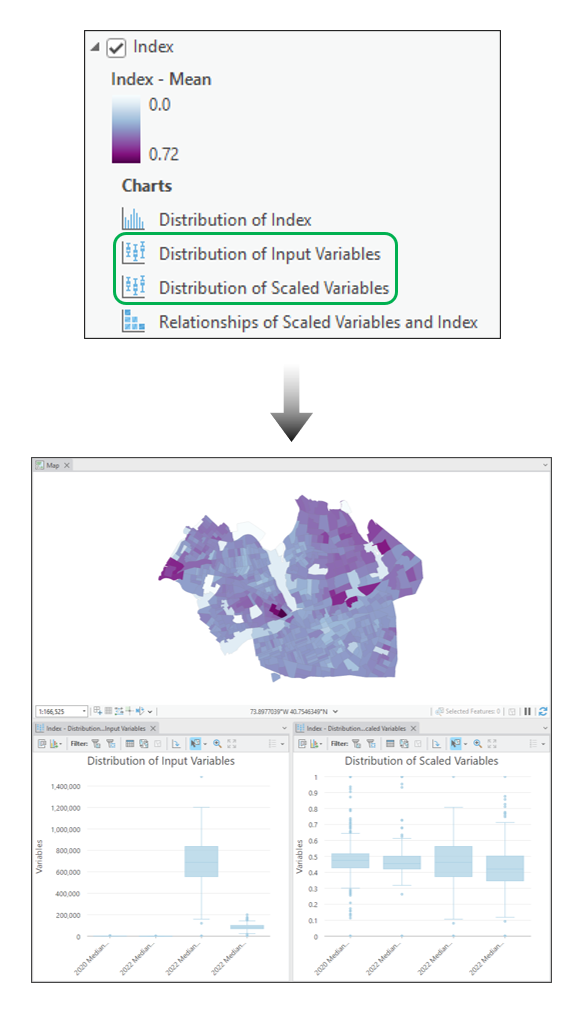
Explorar las distribuciones de las variables de entrada
La capa de índice principal contiene dos diagramas de caja de las variables de entrada: uno que visualiza las distribuciones de las variables antes de escalar y otro que visualiza las distribuciones de las variables después de escalar. A menudo resulta útil comparar estos gráficos en paralelo para evaluar cómo cambió el método de escalado seleccionado las variables de entrada. Comparar estos gráficos en paralelo puede ayudar a evaluar si el método de escalado seleccionado tuvo el efecto previsto en la distribución de las variables.
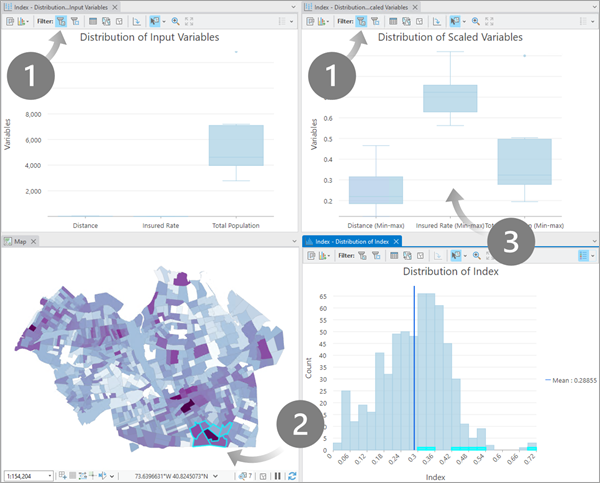
También puede utilizar los diagramas de caja para investigar valores atípicos seleccionando los valores atípicos en el diagrama de caja de variables de entrada y marcando su ubicación en el mapa. A continuación, puede ver el diagrama de caja de variables preprocesadas para comprobar si el método de preprocesamiento elegido ha corregido el efecto del valor atípico.
Explorar los resultados de cada entidad
Al abrir el mapa, el histograma y los dos diagramas de caja y después activar filtros de selección en los dos diagramas de caja, puede seleccionar una entidad en el mapa o en el histograma para visualizar la distribución de los valores de variables de entrada de la selección. También puede usar el mapa y los filtros de extensión en los diagramas de caja para evaluar la distribución de variables en distintas regiones del mapa.
Explorar qué variables afectan al índice
La capa de índice incluye una matriz de gráficos de dispersión que muestra la correlación entre el índice y cada variable utilizada. Las variables con una alta correlación con el índice se corresponden generalmente con las variables que contribuyeron de forma más significativa al índice. Por consiguiente, se puede considerar que cualquier variable con poca correlación con el índice tiene poco impacto en el índice. Además, considere si alguna variable tiene una variación interna baja; es menos probable que las variables con una variación baja aporten información significativa al índice.
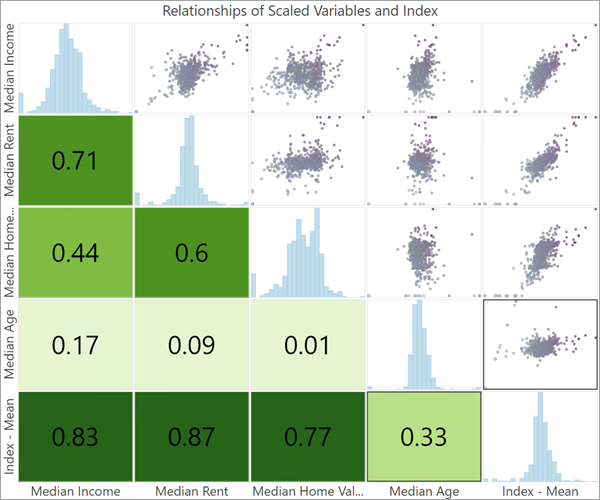
Los mapas y visualizaciones de datos resultantes contribuyen a seguir ajustando y perfeccionando el índice. Para obtener más información sobre consideraciones adicionales a la hora de crear y evaluar un índice, consulte el documento técnico sobre prácticas recomendadas.
Recursos adicionales
Consulte el Manual de construcción de indicadores compuestos: metodología y guía del usuario de la Organización para la Cooperación y el Desarrollo Económicos.