Cómo funciona la densidad kernel

La herramienta Densidad kernel calcula la densidad de las entidades en la vecindad de esas entidades. Puede calcularse para las entidades de punto y de línea.

Los posibles usos incluyen analizar la densidad de las casas o la incidencia de delitos para la planificación social, así como descubrir cómo las líneas de carreteras o de servicios públicos influyen en el hábitat natural. El campo de población se puede utilizar para ponderar algunas entidades más que otras o para permitir que un punto represente varias observaciones. Por ejemplo, una dirección puede representar un condominio con seis unidades, o algunos crímenes se pueden ponderar más que otros al determinar los niveles de crímenes en general. En el caso de las entidades de línea, es posible que una autovía tenga más impacto que un camino estrecho sin asfaltar.

Cómo se calcula la densidad kernel

La densidad kernel se calcula de forma diferente para entidades diferentes.

Entidades de puntos

Densidad kernel calcula la densidad de las entidades de punto de alrededor de cada celda ráster de salida.

Conceptualmente, se ajusta una superficie curva uniforme sobre cada punto. El valor de superficie es más alto en la ubicación del punto y disminuye a medida que aumenta la distancia desde el punto, alcanza cero en la distancia Radio de búsqueda desde el punto. Sólo es posible un vecindario circular. El volumen bajo la superficie es igual al valor Campo de población del punto, o 1 si se especifica NONE. Para calcular la densidad de cada celda ráster de salida, se agregan los valores de todas las superficies de kernel en donde se superponen con el centro de la celda ráster. La función kernel se basa en la función kernel cuártica que se describió en Silverman (1986, p. 76, ecuación 4.5).

Si se utiliza una configuración de campo de población que no sea NONE, el valor de cada elemento determina la cantidad de veces que se va a contar el punto. Por ejemplo, un valor de 3 hará que el punto se cuente como tres puntos. Los valores pueden ser de tipo entero o punto flotante.

De forma predeterminada, una unidad se selecciona según la unidad lineal de la definición de proyección de los datos de la entidad de punto de entrada o como se haya especificado en la configuración del entorno del Sistema de coordenadas de salida.

Si se selecciona un factor de Unidades de área de salida, la densidad que se calculó para la celda se multiplica por el factor apropiado antes de que se escriba en el ráster de salida. Por ejemplo, si las unidades de entrada son metros, las unidades de área de salida serán Kilómetros cuadrados de manera predeterminada. El resultado final de la comparación de un factor de escala de unidades de metros a kilómetros tendrá como resultado que los valores serán diferentes por un multiplicador de 1.000.000 (1.000 metros × 1.000 metros).

Entidades de línea

La Densidad kernel también puede calcular la densidad de las entidades lineales en la vecindad de cada celda ráster de salida.

Conceptualmente, se ajusta una superficie curva uniforme sobre cada línea. Su valor es más grande en la línea y disminuye a medida que se aleja de dicha línea, alcanza cero en la distancia Radio de búsqueda que se especificó desde la línea. La superficie se define de modo que el volumen bajo la superficie sea igual al producto de la longitud de línea y el valor Campo de población. Para calcular la densidad de cada celda ráster de salida, se agregan los valores de todas las superficies de kernel en donde se superponen con el centro de la celda ráster. El uso de la función kernel para las líneas se adapta desde la función de kernel de cuarto grado para las densidades de punto como se describe en Silverman (1986, p. 76, ecuación 4.5).

Se muestra un segmento de línea y la superficie kernel que se ajusta sobre este.

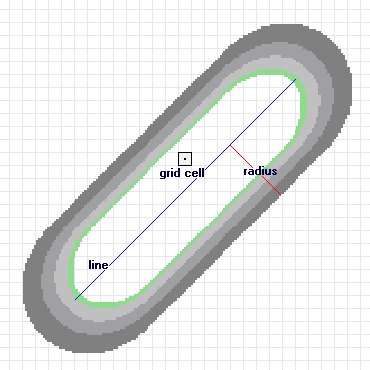
La ilustración anterior muestra un segmento de línea y la superficie kernel que se ajusta sobre el mismo. La contribución del segmento de línea a la densidad es igual al valor de la superficie de kernel en el centro de la celda ráster.

De forma predeterminada, una unidad se selecciona según la unidad lineal de la definición de proyección de los datos de la entidad de polilínea de entrada o como se haya especificado en la configuración del entorno del Sistema de coordenadas de salida.

Cuando se especifica un factor de Unidades de área de salida, este convierte las unidades de longitud y de área. Por ejemplo, si las unidades de entrada son metros, las unidades de área de salida estarán de manera predeterminada en Kilómetros cuadrados y las unidades de densidad de línea resultantes se convertirán a kilómetros por kilómetro cuadrado. El resultado final, al comparar un factor de escala de unidad de metros a kilómetros, será que los valores de densidad serán diferentes por un multiplicador de 1.000.

Puede controlar las unidades de densidad para entidades de punto y línea seleccionando manualmente el factor apropiado. Para establecer que la densidad esté en metros por metro cuadrado (en lugar del valor predeterminado de kilómetros por kilómetro cuadrado), establezca las unidades de área en Metros cuadrados. Del mismo modo, para que las unidades de densidad de la salida estén en millas por milla cuadrada, establezca las unidades de área en Millas cuadradas.

Si se utiliza un campo de población que no sea NONE, se considera que la longitud de la línea es su longitud real multiplicada por el valor del campo de población para esa línea.

Fórmulas para calcular la densidad kernel

Estas fórmulas definen cómo se calcula la densidad kernel para puntos y cómo se determina el radio de búsqueda predeterminado en la fórmula de densidad kernel.

Predecir la densidad de puntos

La densidad prevista en una nueva ubicación (x,y) se determina con esta fórmula:

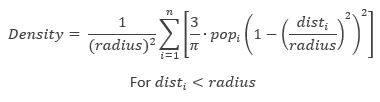
donde:

• i = 1,…,n son los puntos de entrada. Solo debe incluir puntos en la suma si están dentro de la distancia de radio de la ubicación (x,y).
• pop_i es el valor de campo de población del punto i, que es un parámetro opcional.
• dist_i es la distancia entre el punto i y la ubicación (x,y).

Posteriormente, la densidad calculada se multiplica por el número de puntos o la suma del campo de población si se proporcionó alguno. Esta corrección hace que el integral espacial sea igual que el número de puntos (o la suma o el campo de población) en lugar de que siempre sea igual que 1. Esta implementación usa una función kernel cuártica (Silverman, 1986). Será necesario calcular la fórmula para cada ubicación en la que desea estimar la densidad. Puesto que se está creando un ráster, los cálculos se aplican al centro de cada celda en el ráster de salida.

Radio de búsqueda predeterminado (ancho de banda)

El algoritmo que se usa para determinar el radio predeterminado de búsqueda, también conocido como ancho de banda, hace lo siguiente:

1. Calcula el centro medio de los puntos de entrada. Si se proporcionó un campo de Población, este cálculo y los siguientes se ponderarán con los valores de ese campo.
2. Calcula la distancia desde el centro medio (ponderado) para todos los puntos.
3. Calcula la mediana (ponderada) de estas distancias, D_m.
4. Calcula la distancia estándar (ponderada), SD.

   Consulte la herramienta de Estadísticas espaciales Distancia estándar para obtener más detalles sobre el tema.

5. Aplica la fórmula siguiente para calcular el ancho de banda.

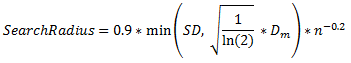
donde:

• D_m es la distancia mediana (ponderada) desde el centro medio (ponderado).
• n es el número de puntos si no se usa ningún campo de población, o si se proporciona un campo de población, la suma de los valores de campo de población.
• SD es la distancia estándar.

Tenga en cuenta que la parte min de la ecuación significa que se utilizará la opción cuyo resultado sea el menor valor de cualquiera de las dos, ya sea SD u .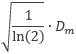

Existen dos métodos para calcular la distancia estándar, sin ponderar y ponderado.

Distancia sin ponderar

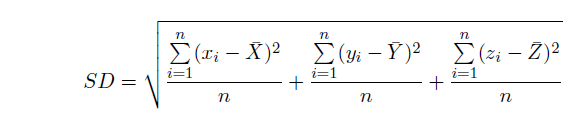
donde:

• x _i , y _i y z _i son las coordenadas de la entidad i
• {x̄, ȳ, z̄} representa el centro medio de las entidades
• n es igual al número total de entidades.

Distancia ponderada

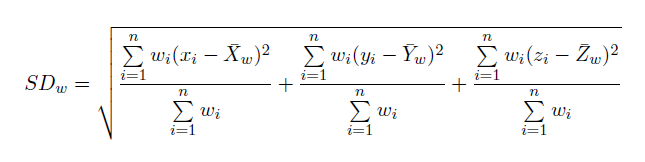
donde:

• w_i es la ponderación de la entidad i
• {x _w, y _w, z _w} representa el centro medio ponderado.

Metodología

Esta metodología para seleccionar el radio de búsqueda se basa en la fórmula de estimación de ancho de banda de la regla general de Silverman, pero se ha adaptado a las dos dimensiones. Por lo general, esta forma de calcular un radio predeterminado evita el fenómeno de generar anillos alrededor de puntos que se produce a menudo con un dataset de puntos dispersos, y es resistente a los valores atípicos espaciales –algunos puntos que están alejados del resto de puntos.

Cómo afecta la barrera al cálculo de la densidad

Las barreras alteran la influencia de las entidades, al mismo tiempo que calculan la densidad kernel para una celda del ráster de salida. Una barrera puede ser una capa de entidades de polilínea o de polígono. Es posible influir en el cálculo de la densidad de dos formas: aumentando la distancia entre la entidad y la celda en la que se está calculando la densidad o excluyendo una entidad del cálculo.

Sin una barrera, la distancia entre una entidad y una celda es la más corta posible, es decir, una línea recta entre dos puntos. Con una barrera abierta, normalmente representada por una polilínea, la ruta entre una entidad y una celda se ve influenciada por la barrera. En este caso, la distancia entre la entidad y la celda se extiende debido a una evitación alrededor de la barrera, como se muestra en la siguiente ilustración. Como resultado, la influencia de la entidad se reduce al estimar la densidad en la celda. La ruta alrededor de la barrera se crea conectando una serie de líneas rectas para ir alrededor de la barrera desde la entidad de punto de entrada hasta la celda. Sigue siendo la distancia más corta alrededor de la barrera, aunque más larga que la distancia que habría sin la barrera. Con una barrera cerrada, normalmente representada por un polígono que abarca completamente algunas entidades, el cálculo de la densidad en una celda en un lado de la barrera excluye completamente las entidades en el otro lado de la barrera.

Se muestra una figura conceptual para el cálculo de la distancia entre una celda y una entidad de punto de entrada. A la izquierda está la densidad kernel sin una barrera; a la derecha, la densidad kernel con una barrera.

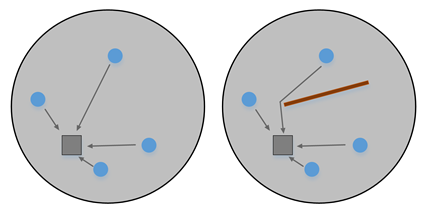
La operación de densidad kernel con una barrera puede proporcionar resultados más realistas y precisos en algunas situaciones, en comparación con la operación de densidad kernel sin una barrera. Por ejemplo, al explorar la densidad de la distribución de una especie de anfibios, la presencia de un acantilado o una carretera puede afectar a su movimiento. El acantilado o la carretera pueden utilizarse como barrera para obtener una mejor estimación de la densidad. De forma similar, el resultado de un análisis de densidad del índice de criminalidad en una ciudad puede variar si se considera como barrera un río que la atraviesa.

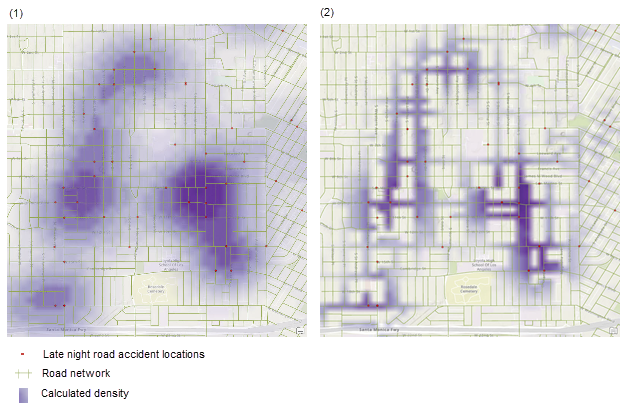
La siguiente ilustración muestra la salida de densidad kernel de accidentes de tráfico nocturnos en Los Ángeles (datos disponibles en el Portal de datos SIG del condado de Los Ángeles). La estimación de la densidad sin una barrera se incluye en la parte izquierda (1) y con una barrera en ambos lados de las carreteras se incluye en el lado derecho (2). La herramienta ofrece una estimación de la densidad bastante mejorada utilizando la barrera, donde la distancia se mide junto con la red de carreteras en vez de utilizar la distancia más corta entre las ubicaciones de los accidentes.

La estimación de la densidad kernel se muestra sin una barrera (1), y con una barrera en ambos lados de las carreteras (2).

Referencias

Silverman, B. W. Density Estimation for Statistics and Data Analysis. New York: Chapman and Hall, 1986.