ArcGIS Network Analyst extension supports six types of solvers that allow you to perform analysis on transportation networks, such as finding the best route across a city, finding the closest emergency vehicle or facility, identifying a service area around a location, or servicing a set of orders with a fleet of vehicles. The sections below describe each solver and the type of network analysis that can be performed.
Learn more about working with the solvers
Route
The route solver can be used to find the best way to get from one location to another or to visit several locations. The best route can be the quickest route for a given time of day considering the traffic conditions applicable during that time, or it can be the shortest route that minimizes the travel distance. The route solver can also find the best route that visits each stop during permitted time windows you specify. If you have more than two stops to visit, the best route can be determined for the fixed order of locations you specify. Such a route is called a simple route. Alternatively, the route solver can determine the best sequence in which to visit the locations (the traveling salesman problem). Such a route is called an optimized route.
Inputs and outputs
The solver has the following input and output parameters:
- Stops (input)—Input locations the route or routes will visit
- Routes (output)—The resulting route, or routes, from the analysis
The route solver can generate turn-by-turn directions for each route in the solution.
For more information about inputs and outputs, see Route analysis layer.
To use the arcpy.nax module for route analysis, see Route input data types and Route output data types.
Closest facility
The closest facility solver measures the cost of traveling between incidents and facilities and determines which are nearest to one other. When finding closest facilities, you can specify how many to find and whether the direction of travel is toward or away from them. The closest facility solver displays the best routes between incidents and facilities, reports their travel costs, and returns driving directions.
When finding the closest facility, you can specify constraints, such as a cutoff cost beyond which the solver does not search for facilities. For instance, you can set up a closest facility problem to search for hospitals within a 15-minute drive of the site of an accident. Any hospitals that take longer than 15 minutes to reach are not included in the results. In this example, the hospitals are facilities, and the accident is the incident. You can also perform multiple closest facility analyses simultaneously. This means you can have multiple incidents and find the closest facility (or facilities) for each incident.
Tip:
The closest facility and OD cost matrix solvers perform very similar analyses; the main difference, however, is in the output and the computation speed. OD cost matrix generates results more quickly but cannot return the true shapes of routes or their driving directions. It is designed to quickly solve large M x N problems and, as a result, does not internally contain the information required to generate route shapes and driving directions. Alternatively, the closest facility solver returns routes and directions but performs the analysis more slowly than the OD cost matrix solver. If you need driving directions or true shapes of routes, use the closest facility solver; otherwise, use the OD cost matrix solver to reduce the computation time.
Inputs and outputs
The solver has the following input and output parameters:
- Facilities (input)—Input locations that are used as the starting or ending points in closest facility analyses
- Incidents (input)—Input locations that are used as starting or ending points in closest facility analyses
- Routes (output)—The resulting route, or routes, of the analysis
The closest facility solver can generate turn-by-turn directions for each route in the solution.
For more information about inputs and outputs, see Closest facility analysis layer.
To use the arcpy.nax module for closest facility analysis, see ClosestFacility input data types and ClosestFacility output data types.
Service area
The service area solver can help you answer the following types of questions:
- How far can I drive from here in 5 minutes?
- What areas are covered within a 3-mile drive distance of my stores?
- What areas are within 4 minutes of our fire stations?
Creating a service area is like buffering a point. When you buffer a point, you specify a straight-line distance, and a circle is created to show the area within that distance. When you create a service area around a point, you also specify a distance, but unlike a buffer, it represents the maximum distance that can be traveled along a network, such as a road network. The result is a service area covering the roads that can be reached within the distance you specified.
For example, the following image compares a 5-mile buffer (the dark circle) with a 5-mile service area (the lighter-colored irregular shape within the buffer):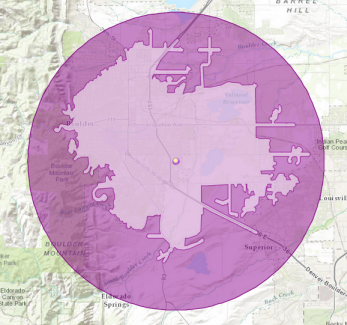 
Service areas model the movement of people or things that move along networks. Buffers assume unimpeded movement in any direction.
For example, to find the number of people within a 5-mile drive of an urgent care facility, it's better to measure the distance along roads using a service area to model the movement of potential patients. Counting the population using a straight-line buffer would overstate the count of those who could truly reach the facility within a 5-mile travel distance.
To customize a service area, set properties on a service area analysis layer and set field values on the features classes that make up the analysis layer.
Inputs and outputs
The solver has the following input and output parameters:
- Facilities (input)—The input facilities around which the output service area polygons are created
- Polygons (output)—The resultant service area polygons, which cover the areas of the network that can be reached within the given time, distance, or other travel-cost cutoff
- Lines (output)—The resultant service areas as linear features that cover the streets, or network edges, that can be reached within the given time, distance, or other travel-cost cutoff
For more information about inputs and outputs, see Service area analysis layer.
To use the arcpy.nax module for service area analysis, see ServiceArea input data types and ServiceArea output data types.
Location-allocation
Location is often considered the most important factor leading to the success of a private- or public-sector organization. Private-sector organizations can profit from a good location, whether a small coffee shop with a local clientele or a multinational network of factories with distribution centers and a worldwide chain of retail outlets. Location can help keep fixed and overhead costs low and accessibility high. Public-sector facilities, such as schools, hospitals, libraries, fire stations, and emergency response services (ERS) centers, can provide high-quality service to the community at a low cost when a good location is chosen.
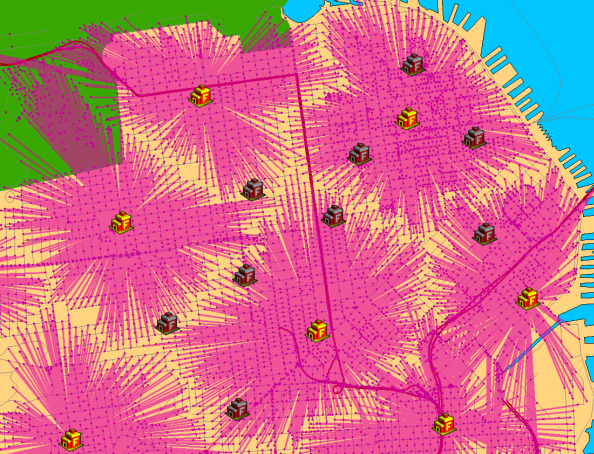
Given facilities that provide goods and services and a set of demand points that consume them, the goal of the location-allocation solver is to locate the facilities in a way that supplies the demand points most efficiently. As the name suggests, location-allocation is a twofold problem that simultaneously locates facilities and allocates demand points to the facilities.
Initially, it may appear that all location-allocation analyses solve the same problem, but the best location is not the same for all types of facilities. For instance, the best location for an ERS center is different than the best location for a manufacturing plant. The next two examples demonstrate how the goals of location-allocation problems vary according to the type of facility being located.
Example 1: Locate an ERS center
When someone calls for an ambulance, they trust it will come to their aid almost instantly; the emergency response time depends considerably on the distance between the ambulance and the patient. Typically, the goal for determining the best sites for ERS centers is to make it possible for ambulances to reach the most people within a defined time frame. The specific question may be: Where should three ERS facilities be placed so the greatest number of people in the community can be reached within four minutes?
Example 2: Locate a manufacturing plant
Many retail outlets receive their goods from manufacturing plants. Whether producing automobiles, appliances, or packaged food, a manufacturing plant can spend a large percentage of its budget on transportation. The location-allocation solver can answer the following question: Where should the manufacturing plant be located to minimize overall transportation costs?
Location-allocation problem types
The Location-Allocation analysis layer includes seven problem types to answer specific types of questions, including questions such as those posed in the two examples above. The seven problem types are the following:
- Minimize Weighted Impedance (P-Median)
- Maximize Coverage
- Maximize Coverage and Minimize Facilities
- Maximize Attendance
- Maximize Market Share
- Target Market Share
- Maximize Capacitated Coverage
Input and outputs
The solver has the following input and output parameters:
- Facilities (input)—Input locations used as the candidate, required, or a competitor facility from which the actual locations will be chosen from in location-allocation analyses
- Demand Points (input)—A location that represents the people or things requiring the goods and services your facilities provide
- Lines (output)—Line features that connect demand points to the facilities to which they are allocated
For more information about inputs and outputs, see Location-Allocation analysis layer.
To use the arcpy.nax module for location-allocation analysis, see LocationAllocation input data types and LocationAllocation output data types.
Origin destination cost matrix
An origin destination (OD) cost matrix solver finds and measures the least-cost paths along the network from multiple origins to multiple destinations. When configuring an OD cost matrix analysis, you can specify the number of destinations to find as well as a maximum distance to search.
Even though the OD cost matrix solver doesn't output lines that follow the network, the values stored in the Lines attribute table reflect the network distance, not the straight-line distance. The results of OD cost matrix analyses often become input for other spatial analyses in which the network cost is more appropriate than straight-line cost. For example, predicting the movement of people in a built environment is better modeled with network costs, since people tend to travel on roads and pedestrian paths.
Tip:
Consider using the Generate Near Table geoprocessing tool instead if finding the straight-line distances better fits your needs.
Tip:
The closest facility and OD cost matrix solvers perform very similar analyses; the main difference, however, is in the output and the computation speed. OD cost matrix generates results more quickly but cannot return the true shapes of routes or their driving directions. It is designed to quickly solve large M x N problems and, as a result, does not internally contain the information required to generate route shapes and driving directions. Alternatively, the closest facility solver returns routes and directions but performs the analysis more slowly than the OD cost matrix solver. If you need driving directions or true shapes of routes, use the closest facility solver; otherwise, use the OD cost matrix solver to reduce the computation time.
Inputs and outputs
The solver has the following input and output parameters:
- Origins—The input locations that function as starting points in generating the paths to destinations
- Destinations—The input locations that function as ending points in generating the paths from origins
- Lines—Lines representing connections between origins and destinations and the travel time or distance between them
For more information about inputs and outputs, see OD Cost Matrix analysis layer.
To use the arcpy.nax module for OD cost matrix analysis, see OriginDestinationCost Matrix input data types and OriginDestinationCost Matrix output data types.
Vehicle routing problem
Various organizations service orders with a fleet of vehicles. For example, a large furniture store might use several trucks to deliver furniture to homes. A specialized grease-recycling company might route trucks from a facility to pick up used grease from restaurants. A health department might schedule daily inspection visits for each of its health inspectors.
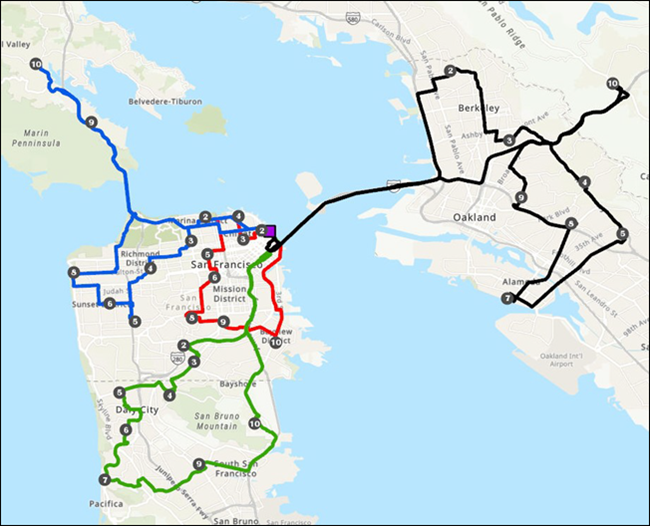
The problem that is common to the examples mentioned above is the vehicle routing problem (VRP). Each organization needs to determine which orders (homes, restaurants, or inspection sites) should be serviced by each route (truck or inspector) and in what sequence the orders should be visited. The primary goal is to best service the orders and minimize the overall operating cost for the fleet of vehicles. Thus, while the Network Analyst route solver finds the best route for a single vehicle to visit many stops, the VRP solver finds the best routes for a fleet of vehicles to service many orders. In addition, the VRP solver can solve more specific problems because numerous options are available, such as matching vehicle capacities with order quantities, giving breaks to drivers, and pairing orders so they are serviced by the same route.
Inputs and outputs
The solver has the following input and output parameters:
- Orders (input/output)—One or more locations that the routes of the VRP analysis will visit. An order can be a delivery to a customer, a pickup from a customer, or some other type of work.
- Depots (input/output)—A location that a vehicle departs from at the beginning of its workday and returns to at the end of the workday.
- Routes (input/output)—One or more routes that specify the vehicle and driver characteristics, and it represents the traversal between depots and orders.
- Breaks (input/output)—The rest periods, or breaks, for routes in a VRP.
- Route Zones (input)—A work territory for a given route.
- Depot Visits (output)—When a route starts, renews (unloads or reloads), or ends at a depot, a depot visit is created. Depot visit objects provide information regarding why a route visited a depot and what happened there.
- Order Specialties and Route Specialties (input)—Tables that list the specialties that can be required by orders and supported by routes. A route can service an order only if it supports all the specialties required for that order.
- Order Pairs (input)—A table of records that is used to pair delivery and pickup orders so they are serviced by the same route.
- Route Renewals (input)—The intermediate depots that the routes of a VRP analysis can visit to reload and unload items they are delivering or picking up.
The VRP solver can generate turn-by-turn directions for each route in the solution.
For more information about inputs and outputs fields, see the VRP analysis layer.
To use the arcpy.nax module for VRP analysis, see VehicleRoutingProblem input data types and VehicleRoutingProblem output data types.
Last mile delivery
The Last Mile Delivery solver focuses on the subset of vehicle routing problems associated with delivering packages to end customers. Last Mile Delivery problems have a single distribution center from which delivery vehicles are dispatched to visit customer locations. These locations may span urban and rural areas and can vary in density. There can be several customers on a street, but not at every address. Customers may also have time windows which restrict visit times. Delivery companies need to know which customers are serviced by each route (delivery vehicle and driver), and in what sequence to visit the customers. The primary goal is to produce geographically clustered routes that allow the drivers to service many customers while minimizing the overall operating cost for the fleet of vehicles.
Note:
The Vehicle Routing Problem solver is a general purpose solver that can model many routing constraints and objectives. However, some common classes of Vehicle Routing Problem analyses can benefit from a more tailored solution. The Last Mile Delivery solver is especially configured to model package delivery from a single depot. For this specific class of problems, the Last Mile Delivery solver improves on the generic Vehicle Routing Problem solver in terms of ease of use, the quality of the routes produced, and the speed of the solve operation.Inputs and outputs
The solver has the following input and output parameters:
- Orders (input/output)—One or more locations that the routes of the Last Mile Delivery analysis will visit to make a delivery to a customer.
- Depots (input/output)—A location that a vehicle departs from at the beginning of its workday and returns to at the end of the workday.
- Routes (input/output)—One or more routes that specify the vehicle and driver characteristics, and it represents the traversal between depots and orders.
- Zones (input)—A work territory for a given route.
- Depot Visits (output)—When a route starts, renews (unloads or reloads), or ends at a depot, a depot visit is created. Depot visit objects provide information regarding why a route visited a depot and what happened there.
- Order Specialties and Route Specialties (input)—Tables that list the specialties that can be required by orders and supported by routes. A route can service an order only if it supports all the specialties required for that order.
For more information about inputs and outputs fields, see Last mile delivery analysis layer.
To use the arcpy.nax module for last mile delivery analysis, see LastMileDelivery input data types and LastMileDelivery output data types.