The Volume Percentile Contours tool generates polygons that enclose a user-chosen percentage of the raster’s total magnitude by accumulating value × cell area from highest values downward.
Each output polygon at percentile p is the smallest possible footprint whose cells collectively contain at least p percent of the raster’s total volume. When multiple percentiles are specified, output polygons are nested. The innermost (minimum) polygon corresponds to the lowest p and captures the areas with the highest values. The outermost (maximum) polygon corresponds to the highest p and shows the broader envelope that contains the majority of the phenomenon. The area of these polygons reports the physical footprint; it does not equal volume. It is the area within which p percent of volume resides.
When to use
Use the Volume Percentile Contours tool when the question is about the amount, such as the location of the smallest area that contains p percent of the total magnitude. The following are examples:
- Delineate the top 50 percent core of incidents from a crime density raster
- Find 90 percent of expected storm damages in a state or county
- Delineate 95 percent of modeled disease outbreak intensity
- Delineate 95 percent of wildlife home range
Comparison with other contour tools
The Contour and Contour List tools create isolines at numeric intervals you specify. Use these tools when the exact values to extract are known (for example, every 5 meters, or specifically at 10, 25, and 35 meters).
Compared to these tools, the Volume Percentile Contours tool creates polygon contours based on the cumulative volume of the raster values and footprint.
| Characteristic | Contour tool | Contour List tool | Value Percentile Contours tool | Volume Percentile Contours tool |
|---|---|---|---|---|
What you specify: | Fixed interval or base (regular spacing) | Fixed list of values (irregular spacing) | One or more percentile values | One or more percentile values |
Output: | Polygon or Polyline output | Polyline output | Encloses p% of cells | Encloses p% of total volume |
Percentile consideration: | No | No | Yes | Yes |
Magnitude (volume) consideration: | No | No | No | Yes |
Output geometry: | Polylines and polygons | Polylines | Polygons | Polygons |
Multivalue as input: | Yes (many lines using an interval) | Yes (many lines using a list) | Yes (multipercentile input) | Yes (multipercentile input) |
Regular or irregular spacing: | Regular (interval) | Irregular (explicit list) | Irregular | Irregular |
Nested (overlap) behavior: | N/A | N/A | Nested polygons | Nested polygons |
Area units reported: | Same as raster | Not applicable | Planar map unit2 or geodesic m2 | Planar map unit2 or geodesic m2 |
Primary question answered: | Show the isolines at these values at this interval | Show the isolines at these specified values | Where is the top p% of the area by values | Where is p% of the total magnitude concentrated |
Key concepts
This section defines the core ideas that the Volume Percentile Contours tool uses. It covers how the cumulative cell volumes are calculated and how the target volume and threshold are chosen. An example workflow follows these concepts.
Cell volume
Each cell contributes to a tiny chunk of mass (whatever the raster represents). Think of every cell as a box. Its height is the raster value and its footprint is the ground area of each cell. Therefore, volume is height × footprint.
For cell i :
vi = di × Ai
Where:
- di is the raster value at that cell
- Ai is the cell’s area computed using the chosen setting of the Method parameter
By default, the tool uses the Planar option for area calculation.
Total volume
The total volume (Vtotal) of the raster is calculated using the following formula:
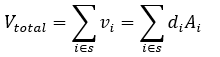
Where:
- S is the set of valid cells.
- vi is the volume of that cell.
- di is the raster value at that cell.
- Ai is the cell’s area computed using the chosen setting of the Method parameter.
By default, the tool uses Planar option for area calculation.
Target volume
For the specified percentile p ∈ (0,100), the tool calculates volume with the following equation:
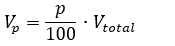
Where:
- p is the percentile value.
- Vp is the target volume at specified percentile.
- Vtotal is the total volume of all the values in the raster.
This is the amount of a phenomenon that will be extracted from the input raster. For example, 50 percent of all crimes, 90 percent of the total probability, or 75 percent of the disaster-affected areas.
Threshold value and volume
The tool sorts cells by value from high to low and finds the smallest value such that keeping all cells at least this high accumulates the target volume. Thus, the following is the definition of the threshold:
Where:
- Tp is the value at the first rank that meets or exceeds the target.
- t is a candidate threshold value the tool considers while searching.
- di is the raster value at that cell.
- Ai is the cell’s area computed using the chosen setting of the Method parameter.
- i:di ≥ t is the set of cells the tool will keep if the cut were i.
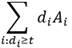is the cumulative volume contributed by cells at or above t.- Vp is the volume of that percentile value.
Cumulative volume
If d1 ≥ d2 ≥ ... ≥ dn is the descending order of all cell values, and the cumulative volume is determined by:
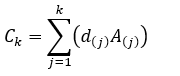
Then the value at the first rank that meets or exceeds the target Tp is determined by:
Tp = dk*
Where:
- k* = min{k:Ck ≥ Vp } is the value at the first rank that meets or exceeds the target
Workflow example
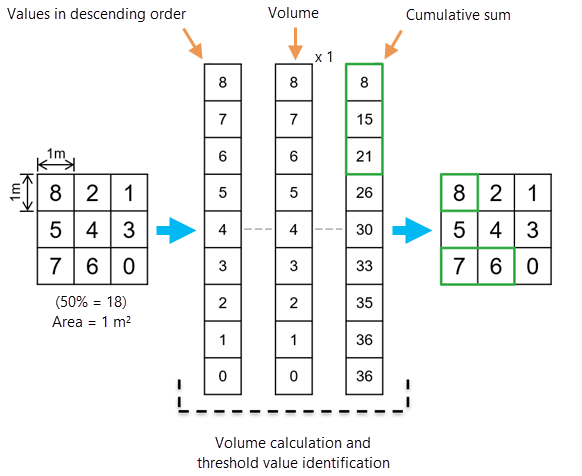
Assume a raster with 9 cells, and each cell has a cell area of 1 (Ai = 1). The following are the raster values:
Row 1: | 8 | 2 | 1 |
Row 2: | 5 | 4 | 3 |
Row 3: | 7 | 6 | 0 |
The value list is: {8, 2, 1, 5, 4, 3, 7, 6, 0}.
The total volume of the raster is:
Vtotal = (8 + 2 + 1 + 5 + 4 + 3 + 7 + 6 +0) × 1 = 36.
The volume percentiles can now be calculated. For example, the following shows 50 percent, 75 percent, and 90 percent of the values:
p = 50 percent: | V50 = 0.50 × 36 = 18 |
p = 75 percent: | V75 = 0.75 × 36 = 27 |
p = 90 percent: | V90 = 0.90 × 36 = 32.4 |
By sorting the cell values in descending order (densest first) and accumulating value × area, you can calculate the cumulative volumes Ck at each value.
| k | Value, d(k) | Ck |
|---|---|---|
1 | 8 | 8 |
2 | 7 | 15 |
3 | 6 | 21 |
4 | 5 | 26 |
5 | 4 | 30 |
6 | 3 | 33 |
7 | 2 | 35 |
8 | 1 | 36 |
9 | 0 | 36 |
To calculate 50th percentile volume contours from the example data, the target volume at that percentile is: 18 (V50 = 18). From the table above, the cumulative volume at k = 2 is 15. This is less than the target volume.
C3 = 15 (< 18)
At k = 3, the cumulative volume is 21. It is larger than the target volume. Therefore, this is the threshold volume and the value (6) at k = 3 will be the threshold value.
C3 = 21 (> 18) => k* = 3
All the values at or above this point will be included in the volume contour.
Handling negative values
The Volume Percentile Contours tool, by definition, sums value × area from the highest values downward until the cumulative volume reaches the target Vp. This assumes the cumulative curve rises as the cells are added.
If all values of the raster are greater than or equal to 0—typical for a density surface—the tool will take the values, sort them in descending order, and calculate the cumulative volume until the target volume (Vp) is reached. This is the standard scenario.
If the input surface raster values are all negative (for example, depth), adding a negative number as the largest value such as -1 actually decreases a signed sum. The Volume Percentile Contour tool handles the negative values in two ways so that the output contour still means the densest core of the phenomenon.
The first way the tool handles negative values is through the Ignore negative values parameter. If the parameter is checked, the tool ignores negative values in the volume calculation and extracts the output contour by only considering positive values. Otherwise, the tool follows a sign-flip method to incorporate negative values to calculate the volume.
Determining threshold with identical values
An input surface raster may have more than one cell with identical values. In such instances, the cumulative volume calculation may grow sharply. As a result, the computed target volume could be within one of these climbs. That means it is not possible to include only a portion of the tied cells at that value while ignoring the others. The tool includes all of these values. The tool identifies the first instance where the running total reaches the target and sets the threshold to that plateau value. Then it selects all cells at or above the initially calculated threshold. As a result, the resultant volume may be over the initially computed threshold.
The tool ensures that the result will never be less than the requested share. However, because it selects all the tied cells at the threshold, in these instances, the output contour may slightly overshoot the percentage. Neighboring percentiles (such as 88 percent or 90 percent) can even produce the same output contour polygon if they all land on the same plateau.
Potential applications
Some potential applications for this tool include the following:
- In ecological research, using species observations density raster, a volume contour can delineate an animal's home range (95 percent volume contour) or core area (50 percent volume contour).
- With crime incident data, create a density surface with the Kernel Density tool. Then use the Volume Percentile Contours tool to delineate the smallest footprint that contains more expected crimes. This supports patrol allocation and strategic planning for crime prevention.
- With wildfire incident data, create a density surface with the Kernel Density tool. On the burn probability raster, use the Volume Percentile Contours tool to identify the 95 percent volume contour. This will show where nearly all expected burning is concentrated. This is useful for wildfire season preparation, response planning, and determining the location for prescribed burns.
- In public health, using patient's location density surface, the Volume Percentile Contours tool could be used to measure access to health-care services or a disease outbreak. A volume contour of 10-20 percent will indicate the compact area containing most expected cases.
Additional resources
See the following for more information:
Gibin, M., Longley, P., and Atkinson, P. (2007). "Kernel density estimation and percent volume contours in general practice catchment area analysis in urban areas." In Proceedings of the GIScience Research UK (GISRUK) Conference, Maynooth, Ireland.
Lewis, D. (2015). "Kernel density estimation and percent volume contours." In C. Brunsdon & A. Singleton (Eds.) Geocomputation: A Practical Primer, 169-184. SAGE Publications.
Kie, J. G., Matthiopoulos, J., Fieberg, J., Powell, R. A., Cagnacci, F., Mitchell, M. S., and Moorcroft, P. R. (2010). "The home-range concept: are traditional estimators still relevant with modern telemetry technology?". Philosophical Transactions of the Royal Society B: Biological Sciences, 365(1550), 2221-2231.