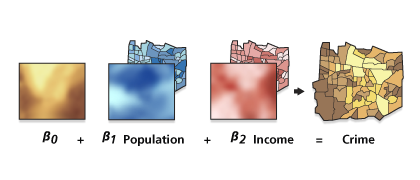
This tool performs Geographically Weighted Regression, a local form of regression used to model spatially varying relationships. The GWR tool provides a local model of the variable or process you are trying to understand or predict by fitting a regression equation to every feature in the dataset. The GWR tool constructs these separate equations by incorporating the dependent and explanatory variables of features within the neighborhood of each target feature. The shape and extent of each neighborhood analyzed is based on the input for the Neighborhood Type and Neighborhood Selection Method parameters with one restriction: when the number of neighboring features will exceed 1000, only the closest 1000 are incorporated into each local equation.
Use this tool on datasets with several hundred features for best results. It is not an appropriate tool for small datasets. The tool does not work with multipoint data.
Use the Input Features parameter with a field representing the phenomena you are modeling (the Dependent Variable value) and one or more fields representing the Explanatory Variable(s) value. These fields must be numeric and have a range of values. Features that contain missing values in the dependent or explanatory variable will be excluded from the analysis; however, you can use the Fill Missing Values tool to complete the dataset before running the GWR tool.
The GWR tool produces a variety of outputs. A summary of the Geographically Weighted Regression model is available as a message at the bottom of the Geoprocessing pane during tool operation. To access the message, hover over the progress bar, click the pop-out button, or expand the messages section in the Geoprocessing pane. You can also access the messages of a previously run GWR tool through the geoprocessing history.
The tool accepts points and polygons as input. For polygons, all distances and neighbors are determined using the distance between polygon centroids (points). However—especially for large, elongated, or multipart polygons—a single point may not be a good representation of the polygon. In these cases, the neighborhoods and the distances between polygons may be unintuitive or misleading. For example, two polygons that share a border may not be considered neighbors if their centroids are far apart. To see the centroids used by this tool, use the Feature To Point tool with the Inside parameter unchecked to convert the polygons to centroid points. You can also use Neighborhood Explorer to visualize the neighborhoods of the polygons or point centroids.
In general, it is not recommended to perform Geographically Weighted Regression on lines because a centroid is rarely an appropriate representation of a line. However, to use lines in the tool, you can use the Feature To Point tool to convert the lines to centroid points and use the centroids in the tool. The results can then be joined back to the original lines.
The Model Type parameter value specified depends on the data you are modeling. It is important to use the correct model for the analysis to obtain accurate results of the regression analysis.
It is recommended that you use projected data. This is especially important when distance is a component of the analysis, as it is for Geographically Weighted Regression when you specify Distance band for the Neighborhood Type parameter. It is recommended that the data be projected using a projected coordinate system (rather than a geographic coordinate system).
Some of the computations can use multiple CPUs to increase performance and will automatically use up to eight threads/CPUs for processing.
It is a common practice to explore data globally using the Generalized Linear Regression tool before exploring data locally using this tool.
The Dependent Variable and Explanatory Variable(s) parameter values should be numeric fields containing a variety of values. There should be variation in these values both globally and locally. For this reason, do not use dummy explanatory variables to represent different spatial regimes in the Geographically Weighted Regression model (such as assigning a value of 1 to census tracts outside the urban core, while all others are assigned a value of 0). Because the GWR tool allows explanatory variable coefficients to vary, these spatial regime explanatory variables are unnecessary, and if included, will create problems with local multicollinearity.
In global regression models, such as Generalized Linear Regression, results are unreliable when two or more variables exhibit multicollinearity (when two or more variables are redundant or together tell the same story). The GWR tool builds a local regression equation for each feature in the dataset. When the values for a particular explanatory variable cluster spatially, it is likely that there are problems with local multicollinearity. The condition number field (COND) in the output feature class indicates when results are unstable due to local multicollinearity. As a general rule, be skeptical of results for features with a condition number greater than 30, equal to Null or, for shapefiles, equal to -1.7976931348623158e+308. The condition number is scale-adjusted to correct for the number of explanatory variables in the model. This allows direct comparison of the condition number between models using different numbers of explanatory variables.
Use caution when including nominal or categorical data in a Geographically Weighted Regression model. Where categories cluster spatially, there is risk of encountering local multicollinearity issues. The condition number included in the Geographically Weighted Regression output indicates when local collinearity is a problem (a condition number less than 0, greater than 30, or set to Null). Results in the presence of local multicollinearity are unstable.
To better understand regional variation among the coefficients of the explanatory variables, examine the optional raster coefficient surfaces created by the GWR tool. These raster surfaces are created in the Coefficient Raster Workspace parameter, under Additional Options, if specified. For polygon data, you can use graduated color or cold-to-hot rendering on each coefficient field in the Output Features value to examine changes across the study area.
You can use the GWR tool for prediction by supplying a Prediction Locations value (often this feature class is the same as the Input Features value), matching the explanatory variables, and specifying an Output Predicted Features value. If the Explanatory Variables to Match fields from the Input Features value match the Fields From Prediction Locations fields, they will automatically populate. If not, specify the correct fields.
A regression model is incorrectly specified if it is missing a key explanatory variable. Statistically significant spatial autocorrelation of the regression residuals or unexpected spatial variation among the coefficients of one or more explanatory variables suggests that the model is incorrectly specified. Make every effort (through Generalized Linear Regression residual analysis and Geographically Weighted Regression coefficient variation analysis, for example) to discover these key missing variables so they can be included in the model.
Determine whether it makes sense for an explanatory variable to be nonstationary. For example, suppose you are modeling the density of a particular plant species as a function of several variables including ASPECT. If you find that the coefficient for the ASPECT variable changes across the study area, you are likely seeing evidence of a key missing explanatory variable (prevalence of competing vegetation, for example). Make every effort to include all key explanatory variables in the regression model.
When the result of a computation is infinity or undefined, the result for nonshapefiles will be Null; for shapefiles, the result will be -DBL_MAX = -1.7976931348623158e+308.
Caution:
Shapefiles cannot store null values. Tools or other procedures that create shapefiles from nonshapefile inputs may, consequently, store null values as zero or as a very small negative number (-DBL_MAX = -1.7976931348623158e+308). This can lead to unexpected results. For more information, see Geoprocessing considerations for shapefile output.
There are three options for the Neighborhood Selection Method parameter. When you specify Golden search, the tool will find the best values for the Distance Band or Number of Neighbors parameter using the golden section search method. The Manual intervals option will test neighborhoods in increments between the distances specified. In either case, the neighborhood size used is the one that minimizes the Akaike information criterion (AICc) value. Problems with local multicollinearity, however, will prevent both of these methods from resolving an optimal distance band or number of neighbors. If you receive an error or encounter severe model design problems, you can try specifying a particular distance or neighborhood count using the User defined option. Then examine the condition numbers in the output feature class to determine which features are associated with local collinearity problems.
Severe model design issues, or errors indicating that local equations do not include enough neighbors, often indicate a problem with global or local multicollinearity. To determine where the problem is, run a global model using the Generalized Linear Regression tool and examine the VIF value for each explanatory variable. If some of the VIF values are large (above 7.5, for example), global multicollinearity is preventing Geographically Weighted Regression from solving. More likely, however, local multicollinearity is the problem. Try creating a thematic map for each explanatory variable. If the map reveals spatial clustering of identical values, consider removing those variables from the model or combining them with other explanatory variables to increase value variation. If, for example, you are modeling home values and have variables for bedrooms and bathrooms, you can combine them to increase value variation or to represent them as bathroom/bedroom square footage. Avoid using spatial regime dummy variables, spatially clustering categorical or nominal variables, or variables with very few possible values when constructing Geographically Weighted Regression models.
Geographically Weighted Regression is a linear model subject to the same requirements as Generalized Linear Regression. Review the diagnostics explained in How Geographically Weighted Regression works to ensure that the Geographically Weighted Regression model is properly specified. The How regression models go bad section in the Regression analysis basics topic also includes information for ensuring that the model is accurate.