Stream ordering is a method of assigning a numeric order to links in a stream network. This order is a method for identifying and classifying types of streams based on their numbers of tributaries. Some characteristics of streams can be inferred by simply knowing their order.
For example, first-order streams are dominated by overland flow of water; they have no upstream concentrated flow. Because of this, they are most susceptible to non-point source pollution problems and can derive more benefit from wide riparian buffers than other areas of the watershed.
The tool has two methods you can use to assign orders. These are the methods proposed by Strahler (1957) and Shreve (1966).
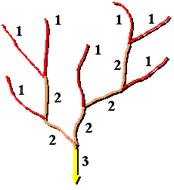
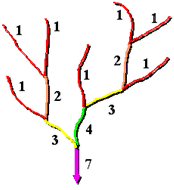
In both methods, the upstream stream segments, or exterior links, are always assigned an order of 1.
Strahler method
In the Strahler method, all links without any tributaries are assigned an order of 1 and are referred to as first order.
The stream order increases when streams of the same order intersect. Therefore, the intersection of two first-order links will create a second-order link, the intersection of two second-order links will create a third-order link, and so on. The intersection of two links of different orders, however, will not result in an increase in order. For example, the intersection of a first-order and second-order link will not create a third-order link but will retain the order of the highest ordered link.
The Strahler method is the most common stream ordering method. However, because this method only increases in order at intersections of the same order, it does not account for all links and can be sensitive to the addition or removal of links.
Shreve method
The Shreve method accounts for all links in the network. As with the Strahler method, all exterior links are assigned an order of 1. For all interior links in the Shreve method, however, the orders are additive. For example, the intersection of two first-order links creates a second-order link, the intersection of a first-order and second-order link creates a third-order link, and the intersection of a second-order and third-order link creates a fifth-order link.
Because the orders are additive, the numbers from the Shreve method are sometimes referred to as magnitudes instead of orders. The magnitude of a link in the Shreve method is the number of upstream links.
References
Tarboton, D. G., R. L. Bras, and I. Rodriguez-Iturbe. 1991. On the Extraction of Channel Networks from Digital Elevation Data. Hydrological Processes. 5: 81–100.