Saison-Trend-Zerlegung mittels LOESS

Saison-Trend-Zerlegung mittels LOESS (STL) ist eine zuverlässige Methode zur Zerlegung von Zeitserien, die häufig bei Wirtschafts- und Umweltanalysen zum Einsatz kommt. Bei der STL-Methode werden lokal angepasste Regressionsmodelle verwendet, um eine Zeitserie in eine saisonale Komponente, eine Trendkomponente und eine Restkomponente zu zerlegen.

STL

STL können Sie auf ein beliebiges Dataset anwenden. Aussagekräftige Ergebnisse erhalten Sie jedoch nur, wenn ein zeitliches Muster in den Daten vorliegt (z. B. eine Abnahme der Luftqualität in den wärmeren Monaten oder eine Zunahme des Online-Shoppings im vierten Quartal jeden Jahres). Das Muster erscheint in den STL-Ergebnissen als die saisonale Komponente.

Der STL-Algorithmus führt in zwei Schleifen eine Glättung der Zeitserie mittels LOESS durch. Die innere Schleife iteriert zwischen der Glättung von saisonalen Schwankungen und der Glättung des Trends. In der äußeren Schleife werden die Auswirkungen von Ausreißern minimiert. Bei der inneren Schleife wird zunächst die saisonale Komponente berechnet und dann entfernt, anschließend erfolgt die Berechnung der Trendkomponente. Der Rest ergibt sich aus der Subtraktion der saisonalen Komponente sowie der Trendkomponente von der Zeitserie.

Die drei Komponenten der STL-Analyse stehen folgendermaßen mit der unverarbeiteten Zeitserie in Beziehung:

yi = si + ti + ri

Dabei gilt:

• y_i = Der Wert der Zeitserie an Punkt i
• s_i = Der Wert der saisonalen Komponente an Punkt i
• t_i = Der Wert der Trendkomponente an Punkt i
• r_i = Der Wert der Restkomponente an Punkt i

Beispiele

Eine Meteorologin untersucht die Auswirkungen des Klimawandels auf die Häufigkeit von Tornados in den Vereinigten Staaten. Anhand von STL zerlegt sie eine Zeitserie mit Tornado-Ereignissen, um zu ermitteln, wie sich saisonale Schwankungen auf die Häufigkeit von Tornados auswirken und ob im Zeitverlauf Tornados mit steigender Häufigkeit verzeichnet wurden. Anschließend kann die Meteorologin die Tornadotrends mit anderen Klimatrends vergleichen, z. B. mit der globalen Durchschnittstemperatur. So kann sie feststellen, ob der Klimawandel bei der zunehmenden Häufigkeit von Tornados ein Faktor ist.

Ein Ökonom verfolgt die Kraftstoffpreise in seiner Region, um im Zeitverlauf Gesamttrends bei der Preisentwicklung aufzudecken. Ihm ist bekannt, dass die Kraftstoffpreise in den Sommermonaten steigen. Daher zerlegt er mittels STL-Analyse die Zeitserie mit den Kraftstoffpreisen und analysiert den Trend gesondert von der saisonalen Komponente.

Saisonale Komponente

Die saisonale Komponente einer STL-Ausgabe zeigt auf Grundlage der ausgewählten saisonalen Schwankungen das wiederkehrende zeitliche Muster in den Daten. Wenn ein saisonales Muster vorhanden ist, weist es i. d. R. die Form einer oszillierenden Kurve bzw. einer Welle auf.

Die Glättung der saisonalen Komponente wird für jede Teilserie (Woche, Monat, Quartal oder Jahr) durchgeführt. Angenommen, Sie führen für ein Dataset mit Daten, die täglich vom Januar 2015 bis zum Dezember 2020 erfasst wurden, eine STL-Analyse mit monatlichen Schwankungen durch. Die Glättung erfolgt dabei zuerst für alle Daten, die in allen Jahren im Januar erfasst wurden, dann für den Monat Februar in allen Jahren usw., bis für alle Monate eine Glättung durchgeführt wurde. Die Teilserien werden anschließend wieder kombiniert und ergeben die saisonale Komponente.

Beispiel

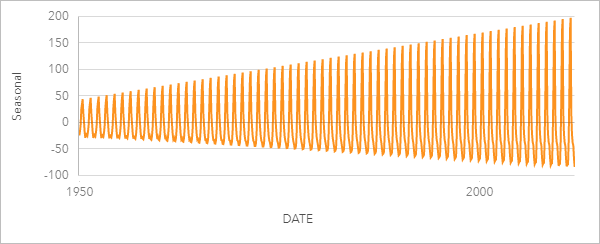
Im folgenden Beispiel sehen Sie die saisonale Komponente einer STL-Analyse von Tornado-Ereignissen in den USA. Die Komponente wurde unter Berücksichtigung von monatlichen saisonalen Schwankungen berechnet. Sie pendelt zwischen einer hohen Anzahl im Juni und einer niedrigen Anzahl im Januar. Die Amplitude der Schwankungen nimmt im Zeitverlauf zu, was bedeutet, dass die saisonalen Unterschiede bei der Tornadohäufigkeit im Zeitverlauf zunehmen.

Trendkomponente

Die Trendkomponente ist die zweite Komponente, die in der inneren Schleife berechnet wird. Die Werte der saisonalen Komponente werden von den unverarbeiteten Daten subtrahiert, wodurch saisonale Unterschiede aus der Zeitserie entfernt werden. Anschließend wird eine geglättete Trendlinie erzeugt, indem die LOESS-Methode auf die verbleibenden Werte angewendet wird.

Beispiel

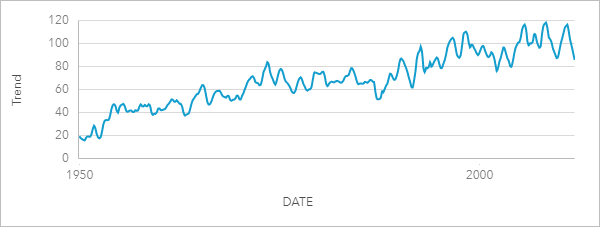
Im folgenden Beispiel sehen Sie die Trendkomponente einer STL-Analyse von Tornado-Ereignissen in den USA. Den Ergebnissen ist ein positiver Gesamttrend zu entnehmen, was bedeutet, dass die Anzahl an Tornado-Ereignissen in den USA im Zeitverlauf steigt.

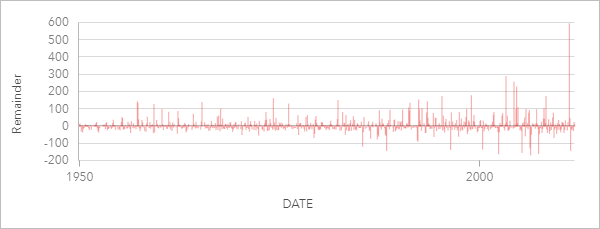
Restkomponente

Die Restkomponente ergibt sich aus der Subtraktion der Werte der saisonalen Komponente sowie der Trendkomponente von der Zeitserie. Die Restwerte stellen den Rauschanteil der Daten dar. Werte nahe 0 bedeuten, dass saisonale Komponente und Trendkomponente eine genaue Beschreibung der Zeitserie darstellen. Höhere Restwerte hingegen deuten auf das Vorhandensein von Rauschen hin.

Anhand der Restkomponente können Sie ebenfalls Ausreißer in den Daten bestimmen. Im Vergleich zu den anderen Restwerten sind dies relativ große positive oder negative Werte.

Beispiel

Im folgenden Beispiel sehen Sie die Restkomponente einer STL-Analyse von Tornado-Ereignissen in den USA. Zu Anfang sind die Restwerte relativ niedrig, steigen aber über die letzten Jahre hinweg an. Dies bedeutet, dass das Rauschen in den Daten im Zeitverlauf zugenommen hat. Den dargestellten Werten lässt sich ein klarer Ausreißer im April 2011 entnehmen.