Die Aggregation von Ereignispunktdaten zu regelmäßig geformten Gittern wird aus vielen Gründen verwendet, beispielsweise zum Normalisieren der Geographie für die Kartenerstellung oder zum Reduzieren der Probleme im Zusammenhang mit der Verwendung unregelmäßig geformter Polygone, die willkürlich erstellt wurden (z. B. Landkreisgrenzen oder Blockgruppen, die aus einem politischen Prozess erstellt wurden). Regelmäßig geformte Gitter können aus gleichseitigen Dreiecken, Quadraten oder Hexagonen bestehen, da nur diese drei Polygon-Shapes mosaikiert werden können (wobei immer wieder dasselbe Shape, Kante an Kante, wiederholt wird, um einen Bereich ohne Lücken oder Überlappungen abzudecken).

Obwohl in GIS-Analysen und thematischen Karten vorwiegend das Quadratgitter (Netz) verwendet wird, gibt es Situationen, in denen Hexagone je nach Problemstellung besser für Analysen geeignet sind.
Eine Aggregation in ein Hexagongitter kann aus folgenden Gründen in Erwägung gezogen werden:
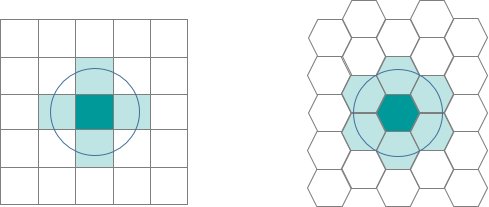
- Hexagone reduzieren die Stichprobenverzerrung aufgrund von Kanteneffekten des Netz-Shape; dies hängt mit dem geringen Umfang-zu-Flächen-Verhältnis des Shape und Hexagons zusammen. Ein Kreis weist das kleinste Verhältnis auf, kann jedoch nicht zu einem kontinuierlichen Gitter mosaikiert werden. Hexagone bilden das kreisförmigste Polygon, das zu einem Gitter mit gleichmäßigen Abständen mosaikiert werden kann.
- Diese Kreisförmigkeit eines Hexagongitters ermöglicht eine natürlichere Darstellung von Kurven in den Mustern Ihrer Daten als bei quadratischen Gittern.
- Wenn Polygone mit gleichen Flächen verglichen werden, gilt Folgendes: Je mehr das Polygon einem Kreis ähnelt, desto näher liegen die in der Nähe der Umrandung gelegenen Punkte am Schwerpunkt (insbesondere Punkte in der Nähe der Stützpunkte). Dies bedeutet, dass jeder Punkt innerhalb eines Hexagons näher am Schwerpunkt des Hexagons liegt als ein bestimmter Punkt in einem Quadrat oder Dreieck mit gleicher Fläche (dies ist auf die spitzen Winkel des Quadrats und Dreieck im Vergleich zum Hexagon zurückzuführen).
- Hexagone sind vorzuziehen, wenn Ihre Analysen Konnektivitätsaspekte oder Bewegungspfade enthalten.
- Aufgrund der linearen Form von Rechtecken, können Netzgitter den Blick auf die geraden, ununterbrochenen, parallelen Linien lenken, die die zugrunde liegenden Muster in den Daten blockieren. Hexagone tendieren dazu, die Linien zu unterbrechen, und ermöglichen eine deutlichere und einfachere Erkennung der Krümmung der Muster in den Daten. Diese Auflösung künstlicher linearer Muster vermindert außerdem jede Ausrichtungsverzerrung, die in Netzgittern wahrgenommen werden kann.
- Wenn Sie mit einer großen Fläche arbeiten, weist ein Hexagon aufgrund der Krümmung der Erde eine geringere Verzerrung auf als das Shape eines Netzgitters.
- Die Suche von Nachbarn ist mit einem Hexagongitter relativ einfach. Da die Kontaktkante oder -länge auf jeder Seite identisch ist, ist der Schwerpunkt jedes Nachbarn äquidistant. Mit einem Netzgitter sind jedoch die Schwerpunkte der "Rook's Case"-Nachbarn (oberhalb/unterhalb/rechts/links) N Einheiten entfernt, während die Schwerpunkte der diagonalen Nachbarn (Queen) weiter entfernt sind (die Entfernung entspricht genau der Quadratwurzel der N-Einheiten, multipliziert mit 2).
- Da die Entfernung zwischen Schwerpunkten bei Hexagonen in allen sechs Richtungen gleich ist, werden bei Verwendung eines Entfernungsbands zum Suchen von Nachbarn oder bei Verwendung des Werkzeugs Optimierte Hot-Spot-Analyse, Optimierte Ausreißeranalyse oder Raum-Zeit-Würfel durch Aggregieren von Punkten erstellen mehr Nachbarn in die Berechnungen für jedes Feature einbezogen, wenn Sie ein Hexagongitter statt ein Netzgitter nutzen.
Zusätzliche Ressourcen:
Birch, Colin P.D., Oom, Sander P., and Beecham, Jonathan A. Rectangular and hexagonal grids used for observation, experiment, and simulation in ecology. Ecological Modelling, Vol. 206, No. 3–4. (August 2007), pp. 347–359.