Das Werkzeug Trend verwendet eine globale Polynominterpolation, die eine glatte, von einer mathematischen Funktion (Polynomfunktion) definierte Oberfläche an die Eingabereferenzpunkte anpasst. Die Trend-Oberfläche ändert sich schrittweise und erfasst grobskalige Muster in den Daten.
Konzeptioneller Hintergrund
Vom Konzept her entspricht die Interpolation mit "Trend" dem Einführen eines Blatt Papiers zwischen die (bis zur Höhe des Wertes) erhöhten Punkte. Dies wird nachstehend für einen Satz von Referenzhöhenpunkten veranschaulicht, die auf einem Hügel mit sanftem Anstieg genommen wurden. Das Stück Papier ist magentarot.
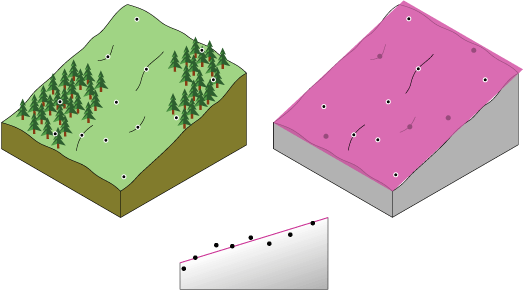
Mit einem flachen Blatt Papier wird eine Landschaft mit einem Tal nicht präzise erfasst. Wenn Sie jedoch das Blatt einmal biegen, erhalten Sie eine bessere Anpassung. Das Hinzufügen eines Terms zur mathematischen Formel liefert ein ähnliches Ergebnis: eine Biegung in der Ebene. Eine flache Ebene (keine Biegung im Blatt Papier) ist ein Polynom erster Ordnung (linear). Das Zulassen von einer Biegung ist ein Polynom zweiter Ordnung (quadratisch), von zwei Biegungen ein Polynom dritter Ordnung (kubisch) usw. Dieses Werkzeug lässt maximal 12 Biegungen (12. Ordnung) zu. Die folgende Abbildung zeigt ein Polynom zweiter Ordnung, das an ein Tal angepasst wurde.
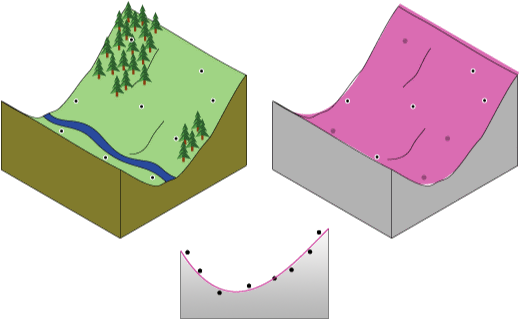
Nur selten verläuft das Blatt Papier durch die tatsächlich gemessenen Punkte, weshalb "Trend" ein ungenauer Interpolator ist. Einige Punkte befinden sich über dem Blatt, andere darunter. Wenn Sie jedoch die Beträge addieren, um die sich jeder Punkt höher über dem Blatt bzw. tiefer unter dem Blatt befindet, sollten die beiden Summen ähnlich sein. Die magentafarben gezeigte Oberfläche wird mithilfe einer Anpassung per Kleinste-Quadrate-Regressionsanalyse erzielt. Die resultierende Oberfläche minimiert die quadrierten Differenzen zwischen den erhöhten Werten und dem Blatt Papier.
Je geringer der RMS-Fehler ist, desto präziser repräsentiert die interpolierte Oberfläche die Eingabepunkte. Die häufigsten Polynomordnungen sind eins bis drei. Oberflächeninterpolationen mit der Funktion "Trend" erstellen glatte Oberflächen.
Verwendung der Trend-Interpolation
Die Interpolation mit "Trend" führt zu einer glatten Oberfläche, die abgestufte Trends auf der Oberfläche im Untersuchungsbereich abbildet. Dieser Interpolationstyp kann für die folgenden Fälle eingesetzt werden:
- Anpassen einer Oberfläche an die Referenzpunkte, wenn sich die Oberfläche im Untersuchungsbereich allmählich von Bereich zu Bereich ändert (z. B. die Verschmutzung auf einem Industriegelände).
- Untersuchen und/oder Entfernen der Auswirkungen von Langzeit- oder globalen Trends. In diesen Fällen wird die Methode häufig als Trendoberflächenanalyse bezeichnet.
Bei der Interpolation mit "Trend" wird eine sich langsam verändernde Oberfläche mithilfe von Polynomen niedriger Ordnung erstellt, die möglicherweise einen physikalischen Prozess beschreiben (z. B. Verschmutzung und Windrichtung). Je komplexer das Polynom ist, desto schwieriger wird es jedoch, ihm eine physikalische Bedeutung zuzuschreiben. Darüber hinaus sind die berechneten Oberflächen sehr anfällig für Ausreißer (extrem hohe und niedrige Werte), insbesondere in den Randbereichen.
Trend-Interpolationstypen
Es gibt zwei grundlegende Trend-Interpolationstypen: Linear und Logistisch.
Linear
Der zur Option Linear der Funktion "Trend" gehörende Oberflächeninterpolator erstellt ein Gleitkomma-Raster. Er verwendet eine polynomische Regression, um eine aus kleinsten Quadraten bestehende Oberfläche an die Eingabepunkte anzupassen. Diese Methode ermöglicht Ihnen die Steuerung der Ordnung des Polynoms, das zum Anpassen der Oberfläche verwendet wird. Um diese Methode besser zu verstehen, betrachten Sie ein Polynom der ersten Ordnung. Eine Oberflächeninterpolation der 1. Ordnung mit der Option "Linear" der Funktion "Trend" führt eine Anpassung der kleinsten Quadrate einer Ebene an die Menge der Eingabepunkte durch.
Oberflächeninterpolationen mit der Funktion "Trend" erstellen glatte Oberflächen. Die erstellte Oberfläche durchläuft nur selten die ursprünglichen Datenpunkte, da eine optimale Anpassung für die gesamte Oberfläche durchgeführt wird. Wenn Sie eine Polynomordnung größer 1 verwenden, erstellt der Interpolator unter Umständen ein Raster, dessen Minimum und Maximum über das in der Eingabedatei der Eingabe-Feature-Daten angegebene Minimum und Maximum hinausgehen.
Logistisch
Die Option Logistisch zum Erstellen einer Trend-Oberfläche eignet sich für die Vorhersage des Vorhandenseins bzw. Fehlens bestimmter Phänomene (in Form einer Wahrscheinlichkeit) für eine bestimmte Menge an Positionen (XY) im Raum. Der Z-Wert ist eine kategorisierte Zufallsvariable mit nur zwei möglichen Ergebnissen, z. B. die Existenz einer bedrohten Art oder die Nichtexistenz dieser Art. Die beiden Z-Werte können als 1 und 0 kodiert werden. Diese Option erstellt ein kontinuierliches Wahrscheinlichkeits-Raster mit Zellenwerten zwischen 1 und 0.
Eine Schätzung der maximalen Wahrscheinlichkeit dient der Berechnung des nicht linearen Wahrscheinlichkeitsoberflächenmodells, ohne das Modell zuerst in ein lineares Format zu konvertieren.
Ausgabe-RMS-Datei
Die Ausgabe-RMS-Datei enthält Informationen zum RMS-Fehler der Interpolation. Hierfür werden die Positionswerte im Eingabe-Dataset mit den entsprechenden Werten in der interpolierten Raster-Oberfläche verglichen.
Mit dem RMS-Fehlerwert können Sie den optimalen Wert für den Parameter {order} der Interpolation ermitteln, indem Sie den Ordnungswert so lange ändern, bis Sie den niedrigsten RMS-Fehler erhalten. Der Chi-Quadrat-Wert wird auch ausgegeben.
Beispiel
Ein Beispiel für die Ausgabe-RMS-Datei bei der Ausführung des Werkzeugs Trend, wobei Polynom-Ordnung auf 3 eingestellt ist:
coef # coef
------ ----------------
0 -1192066.7888371
1 -1.78479492586755
2 -0.195982103615487
3 -8.87072249743903e-1
4 -2.0538267625596e-1
5 -3.85610088343239e-1
6 -1.46420255709888e-2
7 -5.31539027745154e-2
8 -2.59261094879031e-3
9 9.71651459136166e-4
------ ----------------
RMS Error = 296.957857221845
Chi-Square = 17019506.0103975Der vorhergesagte Wert an einer beliebigen Position im Ausgabe-Raster für diesen Trend dritter Ordnung kann ermittelt werden, indem die aus einer Reihe von Gleichungen resultierenden Werte addiert werden. Bei diesen Gleichungen ist x = der Längengrad der Position, y = der Breitengrad und der cn-Term der Koeffizientenwert aus der vorhergehenden Tabelle. Die Gleichungen für diese Interpolation der dritten Ordnung lauten wie folgt:
Prediction(x,y) = c0 +
x·c1 + y·c2 +
x2·c3 + x·y·c4 + y2·c5 +
x3·c6 + x2·y·c7 + x·y2·c8 + y3·c9
Im Prinzip ist der Koeffizient 0 immer der Schnittpunkt. Ab diesem Punkt werden die Terme der ersten Ordnung mit dem höchsten x beginnend und ohne x endend durchlaufen. Es wird zu den Termen der zweiten Ordnung gewechselt, wobei die x erneut nach unten durchlaufen werden. Dieser Vorgang wird ebenfalls für die Terme der dritten Ordnung ausgeführt.
Hinweis:
Diese Gleichungen folgen einem ähnlichen Muster, da die Ordnung zunimmt. Beispielsweise werden bei Angabe der vierten Ordnung fünf weitere Werte in der RMS-Tabelle (die Koeffizienten 10, 11, 12, 13 und 14) und entsprechend mehr Gleichungen angegeben, die sie nutzen.