Mit den Werkzeugen Optimale Regionsverbindungen, Optimaler Pfad als Linie und Optimaler Pfad als Raster können Sie Positionen auf optimale Weise durch einen Pfad miteinander verbinden. Manchmal soll der Pfad allerdings breiter sein als eine schmale Polylinie oder eine einzelne Zelle. Das Ergebnis soll ein breiteres, zweidimensionales Gebiet sein, in dem die gesamten Kosten für den Pfad unterhalb eines bestimmten Schwellenwerts liegen. Ein solches Gebiet wird als Korridor bezeichnet.
Sie können ihn durch Puffern eines optimalen Pfades um eine feste Entfernung erzeugen. Allerdings lassen sich mit dieser Vorgehensweise möglicherweise nicht alle für die Route wesentlichen Aspekte richtig erfassen. Ein einfacher Puffer um einen optimalen Pfad könnte z. B. ein Industriegebiet sein. Dieses in die Planung eines Wildtierkorridors einzubeziehen, wäre jedoch höchst unpassend. Die Breite des Korridors, durch den die Positionen miteinander verbunden werden, sollte sich entsprechend der Rate variieren lassen, durch die die tatsächlichen akkumulierten Kosten von Zelle zu Zelle zwischen den Standorten variieren. Da das Industriegebiet einen hohen Preis für die Wildtiere darstellen würde, würde dieses Gebiet nicht in den Korridor einbezogen.

Der Korridor umfasst alle möglichen Kostenpfade, die geringer sind als die angegebenen akkumulativen Kosten. Zum Definieren des Korridors summiert das Werkzeug Kostengünstigster Korridor die Akkumulationskosten-Raster pro Zelle zwischen den Quellen und wählt die Zellen aus, die unter dem angegebenen Kostenschwellenwert liegen.
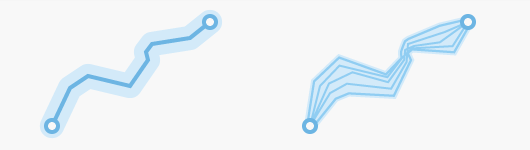
Anwendungsbeispiele für Korridore
Korridore können zur Lösung von Analysen in verschiedenen Szenarien verwendet werden, z. B.:
- Zum Verbinden zweier Bereiche eines Rotwildhabitats in einem Rotwildschutzplan durch den optimalen Korridor.
- Zum Ermitteln der möglichen Route einer geplanten Erdleitung.
- Zum Bestimmen des geeigneten Gebiets, innerhalb dessen ein geplanter Radweg zwischen zwei Parkanlagen verlaufen muss.
Korridoranalyse
Die Entfernungsanalyse kann konzeptionell in die folgenden verwandten Funktionsbereiche unterteilt werden:
- Berechnen Sie die geradlinige Entfernung, und passen Sie die Berechnungen optional mit einem Barriere- oder Oberflächen-Raster an.
- Bestimmen Sie optional durch eine Kostenoberfläche, Quelleneigenschaften, einen vertikalen Faktor und einen horizontalen Faktor die Geschwindigkeit, mit der die Entfernung zurückgelegt wird. Erstellen Sie ein Raster für die akkumulative Entfernung.
- Verbinden Sie Regionen über die resultierende akkumulative Entfernungsoberfläche mithilfe eines optimalen Netzwerks, spezifischer Pfade oder eines Korridors miteinander.
Die Verbindung der Positionen durch Korridore über den dritten Funktionsbereich wird in den folgenden Beispielen dargestellt.
In einem neu eingerichteten Park gibt es eine Bärenpopulation (hellgrünes Polygon) und in der Umgebung einer der vier Ranger-Stationen eine zweite Population (gelber Punkt). Die Bären sollen sich durch einen Korridor zwischen den beiden Positionen bewegen können.
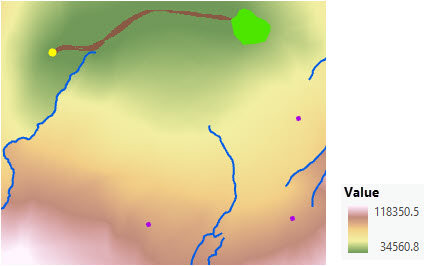
Zwei Raster der akkumulativen Kostenentfernung und zwei Gegenrichtungs-Raster wurden mit dem Werkzeug Entfernungsakkumulation mithilfe von einer Kostenoberfläche, Wasserläufen als Barrieren (blaue Linien) und einem Oberflächen-Raster erstellt. Die vier Raster werden in das Werkzeug Kostengünstigster Korridor eingegeben, und es wird ein Schwellenwert angegeben, um die Breite des Korridors zu definieren.
Erstellen eines Korridors
Allgemeiner Prozess zur Bestimmung eines Korridors zwischen zwei Quellen:
- Berechnen der akkumulierten Entfernung und der Gegenrichtung zwischen der Position der ersten Quelle und allen übrigen Zellen im Untersuchungsgebiet.
- Berechnen der akkumulierten Entfernung und der Gegenrichtung zwischen der Position der zweiten Quelle und allen übrigen Zellen im Untersuchungsgebiet.
- Berechnen der Summe der akkumulierten Entfernungen zwischen den beiden Quellen für jede Zelle.
- Ermitteln der Zellen, deren gesamte akkumulierte Entfernung zwischen den beiden Quellen innerhalb eines definierten Schwellenwerts liegt.
Führen Sie die folgenden Schritte aus, um einen resultierenden Korridor zu erstellen:
Berechnen Sie die Entfernungsakkumulation und die Gegenrichtung für die erste Quelle.
- Öffnen Sie das Werkzeug Entfernungsakkumulation.
- Geben Sie im Parameter Eingabe-Raster oder Feature-Quellen-Daten die erste Position an, die Sie als Quelle (Quelle 1) verbinden möchten.
- Geben Sie einen Namen für das Ausgabe-Entfernungs-Raster für Quelle 1 an.
- Geben Sie im Parameter Eingabe-Kosten-Raster das Kosten-Raster an.
Es ist nicht möglich, eine Bewegungsrichtung in einen Korridor zu integrieren. Folglich dürfen Sie weder einen vertikalen oder horizontalen Faktor noch einen Wert für den Parameter für die Quelleneigenschaft Reiserichtung angeben.
- Geben Sie einen Namen für das Ausgabe-Gegenrichtungs-Raster an.
- Klicken Sie auf Ausführen.
- Öffnen Sie das Werkzeug Entfernungsakkumulation.
- Geben Sie im Parameter Eingabe-Raster oder Feature-Quellen-Daten die zweite Position an, die Sie als Quelle (Quelle 2) verbinden möchten.
- Geben Sie einen Namen für das Ausgabe-Entfernungs-Raster für Quelle 2 an.
- Geben Sie dieselben Parameter an wie in Schritt 4.
- Geben Sie einen Namen für das Ausgabe-Gegenrichtungs-Raster an.
- Klicken Sie auf Ausführen.
- Öffnen Sie das Werkzeug Kostengünstigster Korridor.
- Identifizieren Sie das Ausgabe-Entfernungsakkumulations-Raster für die erste Position (Quelle 1), die in Schritt 6 als Wert des Parameters Eingabe-Raster 1 für akkumulative Kostenentfernung erstellt wurde.
- Identifizieren Sie das Ausgabe-Gegenrichtungs-Raster für die erste Position (Quelle 1), die in Schritt 6 als Wert des Parameters Eingabe-Gegenrichtungs-Raster 1 erstellt wurde.
- Identifizieren Sie das Ausgabe-Entfernungsakkumulations-Raster für die zweite Position (Quelle 2), die in Schritt 12 als Wert des Parameters Eingabe-Raster 2 für akkumulative Kostenentfernung erstellt wurde.
- Identifizieren Sie das Ausgabe-Gegenrichtungs-Raster für die zweite Position (Quelle 2), die in Schritt 12 als Wert des Parameters Eingabe-Gegenrichtungs-Raster 2 erstellt wurde.
- Geben Sie einen Namen für das Ausgabe-Korridor-Raster an.
- Geben Sie die Schwellenwertmethode an. Wählen Sie Kein Schwellenwert, Prozentsatz der Minimalkosten oder Akkumulative Kosten aus.
- Wenn Prozentsatz der Minimalkosten oder Akkumulative Kosten als Schwellenwertmethode ausgewählt ist, geben Sie den Prozentsatz oder den Schwellenwert für akkumulative Kosten an, der zum Definieren der Breite des Korridors verwendet werden soll.
- Klicken Sie auf Ausführen.
Verbinden von Positionen durch die kostengünstigsten Korridore
Ein Korridor definiert den kostengünstigsten geographischen Bereich zur Verbindung zweier Quellenposition. Er enthält alle ungerichteten Kostenpfade zwischen den Quellen, die unter den angegeben akkumulativen Kosten liegen. Der Korridor und die darin enthaltenen Pfade sind ungerichtet, weil die Bewegungsrichtung zwischen den Quellen keine Rolle spielt.
Der Prozess der Korridorerstellung
Zum Erstellen eines Korridor-Rasters benötigen Sie vier Datasets: zwei, die die Eigenschaften der Entfernung zur ersten Quellenposition definieren, und zwei weitere, die die Eigenschaften der Entfernung zur zweiten Position definieren. Mit dem Werkzeug Entfernungsakkumulation erstellen Sie ein Raster mit den akkumulierten Kosten und das Gegenrichtungs-Raster für das erste Quellen-Dataset. Anschließend erstellen Sie mit demselben Werkzeug ein Raster mit den akkumulierten Kosten und ein Gegenrichtungs-Raster für das zweite Quellen-Dataset. Diese beiden Ergebnisse verwenden Sie als Eingaben für das Werkzeug Kostengünstigster Korridor, das dann die Summe der akkumulierten Kosten zwischen den beiden Quellen berechnet und optional einen Schwellenwert anwendet. Zum Erstellen des endgültigen Raster-Ergebnisses werden nur die Zellen ausgewählt, die innerhalb dieses Schwellenwerts liegen.
Festlegen eines Schwellenwerts
Es gibt drei Methoden zum Festlegen eines Schwellenwerts: Kein Schwellenwert, Prozentsatz der Minimalkosten und Akkumulative Kosten.
Wenn die Option Kein Schwellenwert angegeben ist, umfasst der resultierende Korridor die volle Ausdehnung der zwei hinzugefügten Eingabe-Raster mit akkumulativen Kosten.
Wenn Prozentsatz der Minimalkosten angegeben ist, wird der Korridor durch Anwenden des angegebenen Prozentsatzes auf den Minimalwert der Korridoroberfläche erstellt. Wenn ein Prozentsatz von Null oder annähernd Null angegeben wird, werden manche Zellen möglicherweise vom Korridor getrennt. Diese Zellen sind über die Eingabe-Gegenrichtungs-Raster mit dem Korridor verbunden. Weitere Informationen finden Sie weiter unten im Abschnitt Getrennte Zellen im Korridor.
Wenn Akkumulative Kosten ausgewählt ist und ein Schwellenwert angegeben ist, werden zum Erstellen des Korridors alle Zellen ausgewählt, deren akkumulative Kosten kleiner oder gleich dem angegebenen Schwellenwert sind. Der angegebene Schwellenwert muss größer oder gleich dem Minimalwert der Korridoroberfläche sein. Wenn mit den ausgewählten Zellen kein verbundener Korridor zwischen den Eingabequellen erstellt wird, werden sie mithilfe der Eingabe-Gegenrichtungs-Raster verbunden. Weitere Informationen finden Sie weiter unten im Abschnitt Getrennte Zellen im Korridor.
Untersuchen des Korridors
Die nachfolgende Abbildung zeigt ein Beispiel für einen Korridor, der für ein geplantes Bauvorhaben für eine Stromleitung erstellt wurde. Hierbei bilden die Kosten für den Landerwerb das einzige Kriterium zur Bewertung der Kosten für den Korridor. Der endgültige Korridor (hellrot) enthält alle Pfade, deren Kosten maximal 10 Prozent über der vom Minimalwert der Korridoroberfläche abgeleiteten kostengünstigsten Route liegen, die ebenfalls abgebildet ist (dunkelrote Linie). Die Breite des Korridors variiert über seine Länge, und an einigen Stellen gibt es deutliche Abweichungen. Dieses Ergebnis ist anders, als wenn ein Puffer mit fester Breite um die kostengünstigste Route erstellt würde.
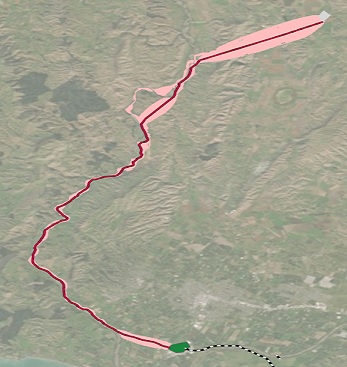
Wenn Sie alle Zellen mit akkumulativen Gesamtkosten auswählen, die maximal 10 Prozent über den Kosten der kostengünstigsten Route liegen, wäre das Ergebnis als 10-Prozent-Kostenkorridor zu betrachten.
Korridorbreite
Schmale Abschnitte eines Korridors sind typischerweise Bereiche, in denen der Korridor am stärksten kostensensibel ist, weil es dort weniger Optionen für Routenverläufe gibt. Im Fall der Stromleitung könnten die schmaleren Abschnitte des Korridors die Positionen sein, die zuerst erworben werden sollten, weil es in diesen Abschnitten des Korridors weniger Spielraum für die Aufstellung von Strommasten gibt. Dies sind die kritischsten Bereiche des Korridors.
Bei der Standortauswahl für Wildtierkorridore sind die schmalen Abschnitte möglicherweise die Stellen, an denen die Tiere am stärksten gefährdet sind, wenn sie sich durch die Landschaft bewegen. Die schmalen Abschnitte müssen am besten geschützt werden, weil hier die Bewegungsoptionen für die Tiere geringer sind.
Eine weitere Möglichkeit, sich die Bedeutung der Korridorbreite vor Augen zu führen, ist die Vorstellung eines Flusses, der durch ein Tal fließt. Die weiten und flachen Stellen des Tals bieten dem Fluss die meisten Optionen, um ungehindert zu fließen. Bei Hochwasser kann der Fluss über die Ufer treten und sich verbreitern oder sogar seinen Lauf ändern. Wenn sich das Tal allerdings zu einer Schlucht mit steil aufsteigenden Wänden verengt, kann der Fluss seinen Lauf weniger gut ändern. Die Kosten, die die engeren Abschnitte der Schlucht verursachen, können als wesentlich höher angesehen werden. Eine visuelle Darstellung dieses Konzepts finden Sie unten im Abschnitt Weitere Informationen. In dieser Visualisierung stellt der Fluss die kostengünstigste Route dar, und die Konturlinien spiegeln die unterschiedlichen Kostenschwellen wider.
Angemessener Schwellenwert
Der Schwellenwert ist abhängig von den Einheiten der Kostenoberfläche. Am einfachsten ist es, wenn die Kosten in Dollar angegeben werden können. Für einen Wildtierkorridor allerdings lässt sich die Kostenschwelle nur schwer bestimmen, wenn die Kosteneinheiten eine Sache der Präferenz sind. Die Zuordnung eines biologischen Schwellenwerts zu subjektiven und präferenzabhängigen Kosteneinheiten ist schwierig zu rechtfertigen.
In solchen Fällen wird so lange mit unterschiedlichen Schwellenwerten experimentiert, bis die angemessenen Bandbreiten ermittelt sind. Idealerweise wird der festgelegte Schwellenwert durch objektive Messwerte bestimmt.
Inseln im Korridor
Je nach festgelegtem Schwellenwert können im resultierenden Korridor Inseln in Bereichen erzeugt werden, in denen sich der Korridor verzweigt und dann die Zweige wieder verbunden werden, ähnlich wie im Beispiel mit der Stromleitung weiter oben. Die Inselzellen sind mit höheren akkumulativen Kosten verbunden und müssen durch den Korridor umgangen werden.
Richtungsabhängigkeit von Korridoren
Da Korridore ungerichtet sind, ist die Bewegung von der ersten zur zweiten Quelle mit denselben Kosten verbunden wie die Bewegung von der zweiten zurück zur ersten. Hier ist es allerdings wichtig, das Werkzeug Entfernungsakkumulation beide Male mit denselben Einstellungen auszuführen.
Über eine Kostenoberfläche und ein Oberflächen-Raster können Sie den Komplexitätsgrad bei der Modellierung der Entfernung erhöhen. Sie können aber keinen vertikalen Faktor, horizontalen Faktor oder die Quelleneigenschaft Reiserichtung verwenden, da diese Parameter auf der Richtungsabhängigkeit der Bewegung beruhen.
Mehrere Quellenpositionen
Die Anzahl der eindeutigen Quellen für die Erstellung der Eingabe-Raster mit akkumulativen Kosten kann durchaus höher sein als eins. In das Werkzeug Entfernungsakkumulation können mehrere Quellen eingegeben werden. Je nach Höhe der akkumulativen Kosten zwischen den Quellen und dem angegebenen Schwellenwert können zwischen den Quellen anstelle eines einzelnen Korridors auch mehrere gebildet werden.
Berechnen der Korridore auf Zellenbasis
Das folgende Diagramm zeigt, wie ein Korridor für eine einzelne Zellenposition erstellt wird. Dieser Prozess wird eigentlich für jede Zelle in den Eingabe-Rastern ausgeführt; zu Demonstrationszwecken wird hier aber nur eine Zelle gezeigt.
Damit ein Korridor erstellt werden kann, müssen mit dem Werkzeug Entfernungsakkumulation ein Raster mit akkumulativen Kosten und ein Gegenrichtungs-Raster von Quelle 1 ausgehend sowie ein Raster mit akkumulativen Kosten und ein Gegenrichtungs-Raster von Quelle 2 ausgehend erstellt werden.
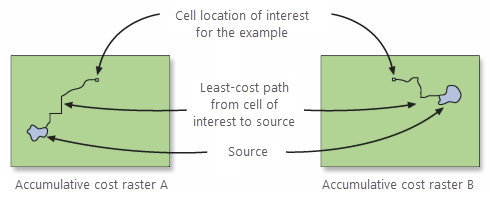
Anschließend werden durch das Werkzeug Kostengünstigster Korridor zwei akkumulative Kostenoberflächen zusammengefügt.
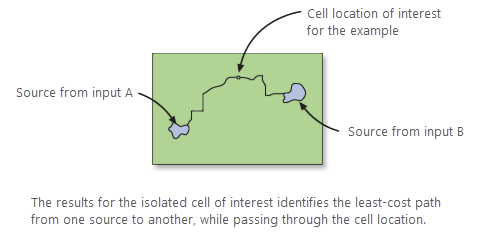
In den summierten Ergebnissen wird nicht nur eine kostengünstigste Route zwischen den beiden Quellen definiert, sondern der gesamte Bereich der akkumulativen Kosten. Das bedeutet, dass die Summe aus den geringsten akkumulativen Kosten für das Erreichen von Quelle 1 und den geringsten akkumulativen Kosten für das Erreichen von Quelle 2 den akkumulativen Gesamtkosten für einen Pfad entspricht, der eine Zelle durchquert. Hierbei handelt es sich um die geringsten akkumulativen Kosten, wenn der Pfad die Zelle zwischen Quelle 1 und Quelle 2 durchquert.
Anschließend wird ein Schwellenwert angewendet, der die Breite des Korridors definiert.
Alle Zellen, deren akkumulative Kosten unter dem angegebenen Schwellenwert liegen, werden aus dem Raster ausgewählt und ergeben einen Korridor. Nach Anwendung des Schwellenwerts kann die resultierende Ausgabe als kostengünstigster Korridor aus Zellen angesehen werden und nicht als kostengünstigste Route (einzelne Linie).
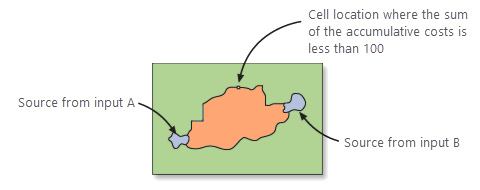
Die zwei Gegenrichtungs-Raster werden verwendet, um sicherzustellen, dass sich keine getrennten Zellen im Korridor befinden. Weitere Informationen finden Sie weiter unten im Abschnitt Getrennte Zellen im Korridor.
Interpretieren von Korridoren
Die Breite eines Korridors kann auf seiner gesamten Länge beträchtlich variieren. Es handelt sich nicht um einen Puffer mit fester Entfernung um eine kostengünstigste Route. Sie können eine erforderliche Mindestbreite definieren und diese festlegen, wenn sich durch eine Reihe von kostengünstigsten Routen ein akzeptabler Korridor bilden lässt.
Eine andere Vorstellung eines Korridors besteht darin, dass er die Unsicherheit hinsichtlich der Position einer kostengünstigsten Route zeigt. Der 10-Prozent-Korridor um eine bestimmte kostengünstigste Route bietet eine gute visuelle Übersicht über alle Pfade, deren Kosten die kostengünstigste Route um nicht mehr als 10 Prozent überschreiten.
Mit einem Korridor lässt sich zeigen, wo die kostengünstigste Route empfindlich auf Änderungen in ihrer Position reagiert. Im obigen Beispiel mit der Stromleitung liegt der breitere Bereich am oberen Ende des Korridors auf weniger teurem Land, sodass es mehr Möglichkeiten gibt, die Position des Pfades in diesem Bereich zu ändern, ohne dass sich die Kosten wesentlich erhöhen. Im Gegensatz dazu sind im schmalen mittleren Abschnitt des Korridors die alternativen kostengünstigsten Routen räumlich beschränkt, sodass es weniger Möglichkeiten gibt.
Weitere Informationen
Die folgenden Abschnitte enthalten weitere Informationen zum Verbinden von Positionen durch Korridore.
Akkumulation der Kostenentfernung anstelle der euklidischen Entfernung
Es gibt zwei Haupttypen für Entfernungsakkumulations-Raster-Ausgaben des Werkzeugs Entfernungsakkumulation: euklidische Entfernung und Kostenentfernung. Die Version mit der euklidischen Entfernung des Entfernungsakkumulations-Rasters wird erstellt, wenn nur Quellen als Eingaben verwendet werden. Die Version mit der Kostenentfernung des Entfernungsakkumulations-Rasters wird meist aus Eingabequellen und einer Kostenoberfläche erstellt.
Wenn die Version mit der euklidischen Entfernung eines Entfernungsakkumulations-Rasters als Eingabe für das Werkzeug Kostengünstigster Korridor verwendet und ein Schwellenwert angegeben wird, hat das Ergebnis Ähnlichkeit mit dem Erstellen eines Puffers um die kürzeste Route zwischen den Quellen. Das Werkzeug Kostengünstigster Korridor ist effektiver für die Kostenentfernungsversion eines Entfernungsakkumulations-Rasters. Die Breite des Korridors ist kein einfacher Puffer, sondern sie basiert auf Kosten. Die Kostenentfernung ist die Rate, mit der die Kosten in jeder Zelle entstehen. Daher basiert die Breite des Korridors darauf, was geschieht, wenn Sie sich von der kostengünstigsten Route weg bewegen.
Getrennte Zellen im Korridor
Das Erstellen eines Korridors entspricht einer zweistufigen Analyse.
Zuerst wird mit dem Werkzeug Entfernungsakkumulation die kostengünstigste Entfernung zu den einzelnen Zellenmittelpunkten im Ausgabe-Raster für akkumulative Kosten berechnet. Zum Bestimmen der kostengünstigsten Entfernung zu den einzelnen Zellen wird die kostengünstigste Route von der kostengünstigsten Quelle zum Zellenmittelpunkt erstellt. Die Berechnung des Pfades erfolgt unabhängig von der Raster-Struktur mithilfe einer numerischen Berechnungsmethode im Werkzeug Entfernungsakkumulation. In der Korridoranalyse ist die ideale kostengünstigste Route zwischen Quelle 1 und Quelle 2 besonders wichtig. Da es in einem Korridor keine Richtungsabhängigkeit gibt, sollten die idealen kostengünstigsten Routen zwischen Quelle 1 und Quelle 2 sowie zwischen Quelle 2 und Quelle 1 identisch sein.
Mit dem Werkzeug Entfernungsakkumulation wird die ideale kostengünstigste Route zwischen den beiden Quellen und der durch die Kostenoberfläche definierten oder in der Analyseumgebung (sowie für alle kostengünstigsten Routen) festgelegten Zellenstruktur kartiert. Bei diesem Rasterungsprozess entsteht eine geringfügige Verzerrung.
Das Werkzeug Kostengünstigster Korridor verwendet die Summe der beiden Eingabe-Raster mit akkumulativen Kosten und erstellt aus dem Minimalwert im Korridor-Raster die ideale kostengünstigste Route zwischen Quelle 1 und Quelle 2 neu. Die abgeleitete ideale kostengünstigste Route dient als Basis für die Bestimmung des Korridors. Mit dem Schwellenwert wird die Breite des Korridors festgelegt, die sich relativ zur abgeleiteten idealen kostengünstigsten Route verhält.
Alle Zellenmittelpunkte, die innerhalb des angegebenen Schwellenwerts liegen, werden in den Korridor einbezogen.
Hinweis:
Die abgeleitete ideale kostengünstigste Route, die vom Werkzeug Kostengünstigster Korridor bestimmt wird, entspricht aus den in diesem Abschnitt genannten Gründen nicht immer der realisierten kostengünstigsten Route aus dem Werkzeug Optimaler Pfad als Linie.
Für einen Korridor gelten zwei Anforderungen:
- Er muss die beiden Eingabequellen verbinden.
- Alle Zellen im Korridor müssen zusammenhängen.
Es gibt jedoch drei Faktoren, die diese beiden Anforderungen erschweren:
- Zellengröße.
- Geringfügige Variabilität der Berechnungen. In der Nähe der Quellen entsteht eine etwas höhere Verzerrung als in größerer Entfernung. Diese geringfügige Verzerrung erhöht die akkumulativen Kosten an diesen Positionen, und die Verzerrung wird etwas verstärkt, wenn die beiden Eingabe-Raster addiert werden.
- Variabilität der Kostenoberfläche, insbesondere in Bereichen mit hohen Kosten.
Aus diesen in Wechselwirkung miteinander stehenden Faktoren ergeben sich zwei Hauptszenarien, durch die getrennte Zellen im Korridor entstehen können. Das Werkzeug Kostengünstigster Korridor stellt sicher, dass diese getrennten Zellen innerhalb des Korridors verbunden sind.
Szenario 1
In diesem Szenario treten die getrennten Zellen entfernt von den Quellen auf. Dort ergibt sich durch die Variabilität der Berechnungen und in Bereichen mit kostenaufwendigen Zellen eine geringere Verzerrung.
Das folgende Beispiel zeigt getrennte Zellen in einem Wildtierkorridor für Schwarzbären. Der Korridor (blauer Bereich) verbindet zwei Lebensräume (violette und gelbe Bereiche). Die (mit dem Pfeil gekennzeichneten) getrennten Zellen in der Mitte des Korridors befinden sich in Bereichen mit kostenaufwendigen Zellen. Diese getrennten Zellen werden vom Werkzeug Kostengünstigster Korridor automatisch mithilfe der Eingabe-Gegenrichtungs-Raster verbunden.
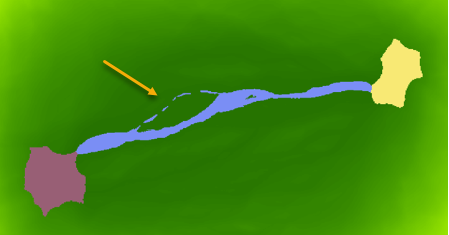
Die Ursache der getrennten Zellen lässt sich am besten anhand eines simulierten Beispiels in der folgenden Abbildung veranschaulichen. Der schwarze Bereich ist der gewünschte Korridor, der ungeachtet der Zellenmittelpunkte in der Korridorkarte durch die angegebenen Schwellenwerte relativ zur abgeleiteten idealen kostengünstigsten Route definiert wird – die Summe der beiden Layer für akkumulative Kosten.

Wie bereits erwähnt, wird die Entfernungsakkumulation zu jedem Zellenmittelpunkt berechnet. In Bereichen mit hohen Kosten versucht die ideale kostengünstigste Route zwischen Quelle 1 und 2 den Weg innerhalb einer kostenaufwendigen Zelle zu begrenzen. Es kann jedoch notwendig sein, einen Teil der Zelle, z. B. eine Ecke, zu durchqueren, wobei nicht die gesamten Kosten bis zum Zellenmittelpunkt entstehen.
Der durch den Schwellenwert definierte Korridor wird (mit der Zellenmittelpunktmethode) wieder den Raster-Zellen des Korridor-Rasters zugeordnet (gerastert). Obwohl der Korridor einen Teil der kostenaufwendigen Zelle durchquert, ist der Zellenmittelpunkt nicht enthalten. Die Zelle wird nicht in den Korridor einbezogen. Dadurch werden bestimmte Zellen vom Korridor getrennt.
Die Eingabe-Gegenrichtungs-Raster kennen jedoch den Weg für die Navigation durch diese kostenaufwendigeren Zellen. Diese Raster werden vom Werkzeug Kostengünstigster Korridor verwendet, um die getrennten Zellen mit dem Korridor zu verbinden. Die akkumulativen Kosten der Zellen, die zum Verbinden dieser getrennten Zellen verwendet werden, liegen etwas über dem angegebenen Schwellenwert.
Um diese Verzerrung zu reduzieren, hätte beim Erstellen der Entfernungsakkumulations-Raster im Werkzeug Entfernungsakkumulation eine geringere Zellengröße verwendet werden können. Durch die geringere Zellengröße können die tatsächlichen niedrigeren akkumulativen Kosten erfasst werden, die in der gröberen Zelle aggregiert wurden, oder die gröbere Zelle wird in kleinere Einheiten unterteilt. Die kostengünstigste Route kann diese kleineren, kostengünstigeren Zellen durchqueren, sodass nicht die gesamten Kosten bis zum Mittelpunkt der Zelle entstehen.
Szenario 2
In diesem Szenario werden getrennte Zellen erstellt, wenn die Methode Akkumulative Kosten verwendet und der Schwellenwert in der Nähe des Minimalwertes auf der Korridoroberfläche festgelegt wird (die Summe der akkumulierten Entfernungs-Raster 1 und 2). Alternativ kann die Methode Prozentsatz der Minimalkosten verwendet und der Prozentsatz auf Null festgelegt werden.
In diesem Szenario leitet das Werkzeug Kostengünstigster Korridor die ideale kostengünstigste Route zwischen den beiden Quellen mithilfe des Minimalwertes der Summe der akkumulativen Raster ab.
Die abgeleitete ideale kostengünstigste Route durchquert die Zellen mit den niedrigsten summierten akkumulativen Kosten und durchquert dabei möglicherweise den Zellenmittelpunkt. Wenn die kostengünstigste Route auf kostenaufwendigere Bereiche trifft, sind die summierten akkumulativen Kosten für die Zellen aus den oben erläuterten Gründen höher als der Minimalwert. Dadurch können getrennte Zellen entstehen. Mithilfe der Gegenrichtungs-Raster stellt das Werkzeug Kostengünstigster Korridor sicher, dass die beiden Quellen mindestens mit einem aus einer einzigen Zelle bestehenden Korridor verbunden sind. Für alle zum Verbinden der getrennten Zellen verwendeten Zellen entstehen etwas über dem Schwellenwert (der Minimalwert im Korridor-Raster) liegende akkumulative Kosten.
In der folgenden Abbildung wird eine generalisierte Version dieses Szenarios gezeigt. Bei der Kostenoberfläche handelt es sich um ein simuliertes Dataset, das alle Zellen mit dem Wert 1 enthält. Die abgeleitete kostengünstigste Route, die die beiden Quellen (rosafarbene Quadrate) verbindet, wird als Linie dargestellt. Die Zellen, die bei einem Schwellenwert von 0 Prozent für den Korridor ausgewählt werden würden, werden schwarz dargestellt. Da die Kostenoberfläche alle Zellen mit dem Wert 1 enthält, ist die abgeleitete kostengünstigste Route eine gerade Linie.

Im Korridor (schwarze Zellen) entstehen Lücken, da die Rasterung zu grob ist. Anfangs wird keine verbundene Sequenz von Zellen ausgewählt. Das Werkzeug Kostengünstigster Korridor verwendet das Gegenrichtungs-Raster zum Verbinden der Zellen, sodass ein kontinuierlicher Korridor entsteht.
Verstehen der Korridore
Um besser verstehen zu können, warum durch Addition der beiden Entfernungsakkumulations-Raster und Festlegung eines Schwellenwerts ein Korridor entsteht, beginnen wir mit dem einfachsten geometrischen Szenario. Eine gerade Linie stellt die kostengünstigste Route zwischen zwei Punkten in einer Ebene dar. Wenn sich Punkt C auf dieser Linie befindet, dann ist AC + CB = AB. In der Terminologie für Korridore ausgedrückt bedeutet das, dass die Summe der akkumulativen Kosten von C nach A und von C nach B konstant ist und zudem den Minimalwert darstellt (also der Länge der Stecke AB entspricht). Folglich ist eine gerade Linie der 0-Prozent-Korridor zwischen A und B. Es gibt noch eine andere Möglichkeit, kostengünstigste Routen zu erstellen, für die kein Gegenrichtungs-Raster erforderlich ist.
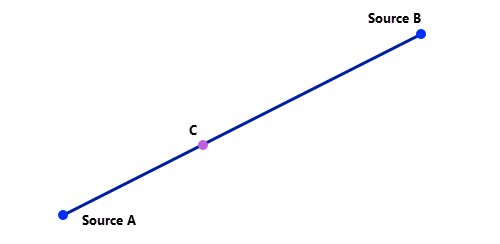
Wenn C von der Linie weg bewegt (also aus der kostengünstigsten Route entfernt) wird, ist AC die neue kostengünstigste Route von C nach A und CB ist die kostengünstigste Route von C nach B. Das Ergebnis lautet: AC + CB > AB. Alle Punkte mit denselben summierten Kosten bilden eine Ellipse um die ursprüngliche kostengünstigste Route. Alle kostengünstigsten Routen, die C mit A und B verbinden, sind im Korridor enthalten. In der Terminologie für Korridore ausgedrückt bedeutet das, dass eine Ellipse der x-Prozent-Korridor um die kostengünstigste Route darstellt. Wie im Beispiel mit der Stromleitung gezeigt, unterscheidet sich am Anfang des Korridors ein kostengünstigster Korridor um eine kostengünstigste Route von einem Puffer mit fester Breite um diese Route.
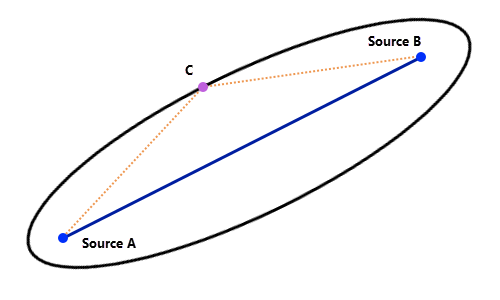
Diese Tatsachen gelten ebenso für allgemeinere kostengünstigste Routen . Der 0-Prozent-Korridor entspricht der kostengünstigsten Route, und Korridore mit größeren Schwellenwerten bilden Konturlinien, die alle Zellen und alle Pfade in diesem Korridor enthalten.
Wenn die Bewegungsrichtung für Ihre Analyse der kostengünstigsten Route unerheblich ist, können Sie mithilfe von Korridoren die Unsicherheit der kostengünstigsten Route oder aller Positionen visualisieren, an denen sich alternative, ungerichtete Pfade befinden könnten, die innerhalb eines akzeptablen Kostenschwellenwerts um die kostengünstigste Route liegen.
Visualisieren von Korridoren
Aus der Darstellung von Korridoren in 3D können Sie Erkenntnisse und neue Perspektiven ableiten. Die kostengünstigste Route ist somit der relativ ebene Grund einer Schlucht, die aus den summierten Eingabeoberflächen für akkumulative Kosten konstruiert wird, und die verschiedenen x-Prozent-Korridore bilden die Konturlinien an den Wänden der Schlucht. Man muss sich von jedem Punkt einer Schluchtwand aus bergab begeben, um zu einer Quelle zu gelangen; das bedeutet, dass man unterhalb der Konturlinie bleiben muss, die den Bereich innerhalb des Prozent-Korridors angibt.

Die breiteren Abschnitte des Korridors aus dem Beispiel mit der Stromleitung befinden sich in dem breiteren, flacheren Becken in der Abbildung oben. Wenn die Bereitschaft besteht, höhere akkumulative Kosten aufzuwenden, kann der Schwellenwert erhöht werden. Die breiteren Becken bieten mehr Möglichkeiten für die Routenführung, da die Breite des Korridors deutlich zunimmt. Die Wände der Schlucht stellen die Bereiche dar, in denen diese Investition weniger erfolgreich sein wird.