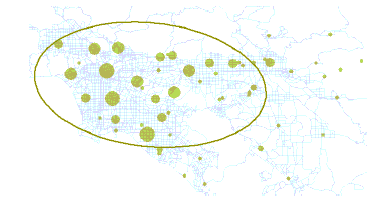
Eine häufige Vorgehensweise beim Messen des Trends für eine Gruppe von Punkten oder Flächen ist die getrennte Berechnung der Standardabweichung in der X-, Y- und Z-Dimension. Anhand dieser Messungen werden die Achsen einer Ellipse (oder eines Ellipsoids) definiert, die die Verteilung von Features umfassen. Die Ellipse wird als Standardabweichungsellipse bezeichnet, da bei dieser Methode die Standardabweichung der X- und Y-Koordinaten vom arithmetischen Mittelpunkt berechnet wird, um die Achsen der Ellipse zu definieren. In 3D wird die Standardabweichung der Z-Koordinaten vom arithmetischen Mittelpunkt ebenfalls berechnet, und das Ergebnis wird als Standardabweichungsellipsoid bezeichnet. Mithilfe der Ellipse oder des Ellipsoids können Sie ermitteln, ob die Feature-Verteilung gestreckt ist und somit eine bestimmte Ausrichtung aufweist.
Sie können zwar einen Eindruck von der Ausrichtung erhalten, indem Sie die Features auf der Karte darstellen, durch die Berechnung der Standardabweichungsellipse wird der Trend jedoch deutlich. Sie können die Standardabweichungsellipse anhand der Positionen der Features oder der Positionen berechnen, die durch einen mit den Features verknüpften Attributwert beeinflusst werden. Letztere Methode wird als gewichtete Standardabweichungsellipse bezeichnet.
Berechnungen
Die Standardabweichungsellipse wird mit den folgenden Formeln berechnet:

Während x und y die Koordinaten für das Feature i sind, stellen {x̄, ȳ} den arithmetischen Mittelpunkt der Features dar und n entspricht der Gesamtzahl der Features.
Die Beispiel-Kovarianzmatrix wird in einem Standardformular berücksichtigt, was dazu führt, dass die Matrix durch Eigenwerte und Eigenvektoren dargestellt wird. Die Standardabweichungen für die X- und Y-Achse lauten dann:
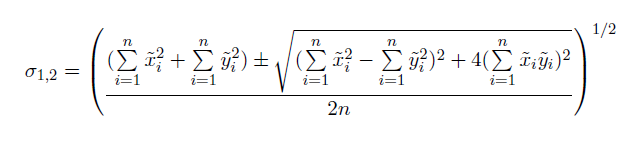
Diese Gleichungen können auf Lösungen für dreidimensionale Daten ausgedehnt werden.
Ausgabe und Interpretation
Mithilfe von Standardabweichungen können Sie die Verteilung von Daten besser verstehen. Beim Arbeiten mit normalverteilten Daten in einer Dimension liegen 68 Prozent, 95 Prozent und 99,7 Prozent der Datenwerte in einer, zwei bzw. drei Standardabweichungen. Wenn jedoch mit höher dimensionalen räumlichen Daten (Y-, Y- und Z-Variablen) gearbeitet wird, sind diese Prozentsätze nicht korrekt. Beispielsweise werden bei normalverteilten Daten in zwei Dimensionen durch eine Standardabweichungsellipse ca. 63 Prozent der Features, durch zwei Standardabweichungen ca. 98 Prozent der Features und durch drei Standardabweichungen ca. 99,9 Prozent der Features abgedeckt. Für drei Dimensionen lauten die entsprechenden Prozentsätze 61, 99 und 100.
Aus diesem Grund werden die Standardabweichungen durch einen Anpassungsfaktor skaliert, um eine Ellipse oder ein Ellipsoid zu erstellen, die bzw. das 68, 95 und 99 Prozent der Features für 2D- und 3D-Daten enthält (unter der Annahme, dass die Daten einer räumlichen Normalverteilung folgen). Diese Anpassungsfaktoren für die Varianzen (die Quadrate der Standardabweichungen) sind in der folgenden Tabelle aufgeführt:
| Eindimensionale Daten | Zweidimensionale Daten | Dreidimensionale Daten | |
|---|---|---|---|
1 Standardabweichung | 1,00 | 1,41 | 1,73 |
2 Standardabweichungen | 2,00 | 2,83 | 3,46 |
3 Standardabweichungen | 3,00 | 4,24 | 5,20 |
Für zweidimensionale Daten erstellt das Werkzeug Richtungsverteilung (Standardabweichungsellipse) eine neue Feature-Class mit einem elliptische Polygon, das auf den arithmetischen Mittelpunkt für alle Features zentriert ist (oder für alle Fälle, in denen ein Wert für den Parameter Case-Feld angegeben wurde). Die Attributwerte für diese Ausgabe-Ellipsenpolygone schließen zwei Standardentfernungen (lange und kurze Achse) ein; die Ausrichtung der Ellipse und ggf. das Case-Feld. Die Ausrichtung stellt die Rotation der langen Achse gemessen im Uhrzeigersinn von 12 Uhr aus dar. Sie können auch die Anzahl der darzustellenden Standardabweichungen (1, 2 oder 3) angeben, um unterschiedliche Prozentsätze der Features abzudecken.
Für dreidimensionale Punktdaten (die Daten sind Z-aktiviert und enthalten 3D-Attributinformationen wie Höhe), erstellt dieses Werkzeug eine neue Feature-Class mit einem Ellipsoid-Multipatch, das auf den arithmetischen Mittelpunkt aller Features zentriert ist (oder für alle Fälle, in denen ein Case-Feld verwendet wird). Die Attributwerte für diese Ausgabe-Ellipsoide schließen drei Standardentfernungen (lange, kurze und hohe Achse) ein; Informationen zum Winkel, zum Rollwinkel des Ellipsoids und ggf. zum Case-Feld. Die Werte für den Winkel, die Neigung und den Rollwinkel des Ellipsoids beschreiben die Ausrichtung des Ellipsoids in einem 3D-Raum. Sie können auch die Anzahl der darzustellenden Standardabweichungen (1, 2 oder 3) angeben, um unterschiedliche Prozentsätze der Features abzudecken.
Potenzielle Anwendungsbereiche
- Durch die Darstellung des Verteilungstrends für eine Reihe von Delikten kann eine Beziehung zu bestimmten physischen Features (eine Reihe von Bars oder Restaurants, ein bestimmter Boulevard usw.) identifiziert werden.
- Durch die Darstellung von Stichproben eines bestimmten Schadstoffs in Grundwasserbrunnen kann die Ausbreitung des Giftstoffs ermittelt werden, was für die Einleitung entsprechender Entschärfungsmaßnahmen hilfreich sein.
- Der Vergleich der Größe, des Shape und der Überlappung von Ellipsen für verschiedene Rassen- und ethnische Gruppen kann Einblicke in die ethnische und Rassentrennung liefern.
- Anhand der Darstellung von Ellipsen für den Ausbruch einer Krankheit im Zeitverlauf lässt sich deren Verbreitung modellieren.
- Die Überprüfung der Höhenverteilung für Stürme einer bestimmten Kategorie kann ein nützlicher Gesichtspunkt sein, der bei der Untersuchung der Beziehung zwischen atmosphärischen Bedingungen und Flugzeugunglücken berücksichtigt werden sollte.
Zusätzliche Quellen
Chew, Victor. "Confidence, prediction, and tolerance regions for the multivariate normal distribution." Journal of the American Statistical Association. 61.315 (1966): 605-617. https://doi.org/10.1080/01621459.1966.10480892.
Fisher, N. I., T. Lewis und B. J. J. Embleton. 1987 "Statistical Analysis of Spherical Data". Erste Ausgabe. Cambridge: Cambridge University Press. Cambridge Books Online. Web. 26. April 2016. https://doi.org/10.1017/CBO9780511623059.
Levine, Ned. "CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004). https://doi.org/10.3886/ICPSR02824.v1.
Wang, Bin, Wenzhong Shi und Zelang Miao. 2015. "Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space". PLoS ONE. 10(3), e0118537.https://doi.org/10.1371/journal.pone.0118537.