Das Werkzeug Kolokalitätsanalyse misst mithilfe der Statistik des Kolokalitätsquotienten lokale Muster der räumlichen Zuordnung zwischen zwei Kategorien von Punkt-Features. Die Ausgabe dieses Werkzeugs ist eine Kartendarstellung der Wahrscheinlichkeit der räumlichen Zuordnung zwischen den beiden Kategorien, die mit zusätzlichen Feldern, einschließlich des Kolokalitätsquotienten und des p-Wertes, analysiert werden. Ein optionaler Tabellenparameter kann festgelegt werden, der Zuordnungen aller Kategorien im Parameter Relevante Eingabe-Features zu allen Kategorien im Parameter Benachbarte Eingabe-Features angibt.
Potenzielle Anwendungsbereiche
Das Werkzeug Kolokalitätsanalyse hat folgende potenzielle Anwendungsbereiche:
- Ist die Wahrscheinlichkeit der Kolokalität bestimmter Unternehmenstypen hoch (z. B. Cafés und Einzelhandelsgeschäfte)?
- Sind Wohnungseinbrüche bei bestimmten Gebäudearten eher wahrscheinlich bzw. liegt eine Kolokalität vor?
- Gibt es bestimmte Bereiche in Ihrem Untersuchungsgebiet, wo eine Kolokalität zwischen Restaurantinspektionen und Beanstandungen mit Insektenbefall vorliegt?
Berechnung des Kolokalitätsquotienten
Jedes Feature in der Interessenskategorie (Kategorie A) wird einzeln auf Kolokalität mit dem Vorhandensein der Nachbarkategorie (Kategorie B) in der Nachbarschaft bewertet. Im Allgemeinen gilt: Wenn der Anteil von B-Punkten in der Nachbarschaft von A größer ist als der globale Anteil von B, ist der Kolokalitätsquotient hoch. Wenn die Nachbarschaft von A viele andere A-Punkte oder viele andere Kategorien außer B enthält, ist die Kolokalität zwischen der Interessenskategorie (Kategorie A) und der Nachbarkategorie (Kategorie B) klein.
Wenn zwei Datasets ohne Kategorien als Eingabetyp verwendet werden, werden die als Relevante Eingabe-Features angegebenen Features als Kategorie A behandelt und die als Benachbarte Eingabe-Features angegebenen als Kategorie B.
Vorsicht:
Die Kolokalitätsbeziehung dieser Analyse ist nicht symmetrisch. Die Werte des Kolokalitätsquotienten beim Vergleichen von Kategorie A mit Kategorie B unterscheiden sich von den Kolokalitätsquotienten beim Vergleichen von Kategorie B mit Kategorie A.
Hinweis:
Wenn die Nachbarschaft Kategorie C enthält, ergeben sich andere Kolokalitätsquotienten, als wenn nur Kategorie A und B vorhanden sind. Je nach Fragestellung sollten Sie möglicherweise eine Teilmenge der Daten extrahieren, die nur die Kategorien A und B enthält. Beim Extrahieren einer Teilmenge gehen jedoch die Informationen über die anderen vorhandenen Kategorien verloren. In Fällen, in denen Sie genau wissen, dass sich das Vorhandensein einer Kategorie nicht auf das Vorhandensein einer anderen Kategorie auswirkt, sollten Sie eine Teilmenge der Daten auswählen und extrahieren.
Der von Punkt Ai in der Interessenskategorie A zur Nachbarkategorie B berechnete Quotient für lokale Kolokalität wird wie folgt angegeben: 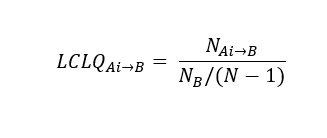
NAi–>B stellt den gewichteten Durchschnitt der Anzahl von Punkten des Typs B in der Nachbarschaft aller Ai dar. Grundlage ist eine Gauß- oder Biquadrat-Kernel-Funktion, die wie folgt ausgedrückt wird: 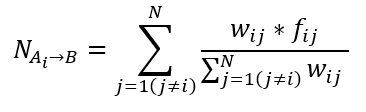
Dabei ist fij eine binäre Variable, mit der angegeben wird, ob Punkt j ein Punkt der Kategorie B ist. Wenn dies zutrifft, ist der Wert 1. Andernfalls ist der Wert 0. Die Gleichungen der Kernel-Funktion werden wie folgt ausgedrückt: 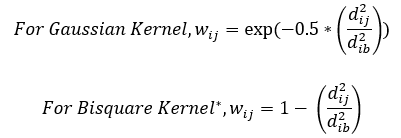
Hinweis:
Wenn der Wert wij für den Biquadrat-Kernel negativ ist, wird die Gewichtung 0 zugewiesen.
Ein Quotient für die globale Kolokalität kann auch berechnet werden, um ein Maß der räumlichen Zuordnung zwischen allen Kategorien im Dataset bereitzustellen. Dies kann Ihnen das Erkunden weiterer Beziehungen in den Daten ermöglichen, wenn Sie global weitere Kategorien mit großer Kolokalität finden. Die Gleichung für den Quotienten für die globale Kolokalität lautet wie folgt: 
Mit Permutationen wird ein p-Wert für jedes relevante Eingabe-Feature berechnet, um zu ermitteln, ob die beobachteten Werte für den Kolokalitätsquotienten statistisch signifikant sind. Für jedes Feature wird der Quotient für die lokale Kolokalität mithilfe der Nachbarschaft berechnet. Für jede Permutation werden die Kategorien aller anderen Punkte nach dem Zufallsprinzip über das gesamte Untersuchungsgebiet neu verteilt (die Kategorie der Zielpunktposition bleibt dabei konstant). Ein neuer Quotient für die lokale Kolokalität wird für jedes relevante Feature berechnet. Dabei werden die Kategorien in der Nachbarschaft für jede Permutation verwendet. Das Ergebnis ist eine Referenzverteilung der Werte von Kolokalitätsquotienten, die daraufhin mit dem tatsächlich beobachteten Wert des Kolokalitätsquotienten für das Feature verglichen werden, um zu bestimmen, mit welcher Wahrscheinlichkeit der beobachtete Wert in der zufälligen Verteilung der Permutationen gefunden werden kann. Wenn Sie sich diese Verteilung ansehen, erkennen Sie den Bereich der Werte des Kolokalitätsquotienten, die das Ergebnis von Zufall sein können. Wenn der p-Wert klein ist (kleiner als 0,05), ist der tatsächliche Kolokalitätsquotient für das Feature statistisch signifikant. Der Standardwert für dieses Werkzeug sind 99 Permutationen. Mit einer größeren Anzahl von Permutationen nimmt die Genauigkeit des berechneten p-Wertes jedoch zu.
Nachbarschaftstyp
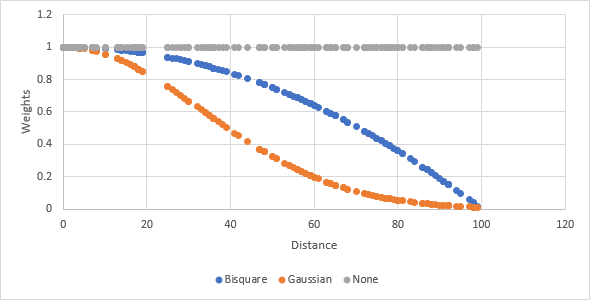
Sie können auf drei Arten einen Nachbarschaftstyp auswählen. Mit einem Entfernungsband wird sichergestellt, dass der Analysemaßstab in allen Nachbarschaften im Untersuchungsgebiet gleich ist. Dies bedeutet, dass für eine Fläche mit einer höheren Dichte mehr Punkte in der Analyse berücksichtigt werden als für Flächen mit einer geringen Dichte. Die Option Nächste Nachbarn (K) ist hinsichtlich der Entfernung anpassbar. Damit wird sichergestellt, dass jede Nachbarschaft für jedes Feature die gleiche Anzahl von Nachbarn enthält. Sie können auch eine mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen erstellte .swm-Datei angeben, um räumliche Gewichtungen auf andere Arten anzugeben.
Verwenden eines Raum-Zeit-Fensters
Wenn Ihre Daten Datums- und Uhrzeitfelder enthalten, können Sie die Analyse in eine Reihe von Raum-Zeit-Fenstern unterteilen. Durch die Angabe von Interessen-Zeitfeld, Nachbarkategorien-Zeitfeld und Typ der zeitlichen Beziehung können Sie steuern, welche Features in die analysierte Nachbarschaft einbezogen werden. Features, die räumlich und zeitlich nahe beieinander liegen, werden zusammen analysiert, da alle Feature-Beziehungen im Hinblick auf die Position und den Zeitstempel des Ziel-Features ausgewertet werden. Im folgenden Beispiel werden mit einem Entfernungsband von 1 Kilometer sechs Nachbarn für das Feature "Jan 31" ermittelt. Im folgenden Beispiel werden mit einem Entfernungsband von 1 Kilometer und einem Raum-Zeit-Fenster von 1 Tag nach dem Ziel-Feature jedoch nur zwei weitere Nachbarn ermitteln.

Nehmen Sie an, Sie würden in einer Region die Waldbrandherde und die Postionen von Campern analysieren. Bei der Ausführung des Werkzeugs Kolokalitätsanalyse nur mit der Option Entfernungsband für Nachbarschaftstyp, um die Feature-Beziehungen zu definieren, wäre das Ergebnis eine Karte, auf der die Positionen der Waldbrandherde dargestellt sind. Zudem wäre angegeben, ob eine Kolokalität mit den in Ihrem Dataset aufgezeichneten Campern vorliegt. Wenn Sie dann die Analyse erneut ausführen würden und dabei ein Raum-Zeit-Fenster mit den obigen Parametern definieren, könnten Sie sicherstellen, dass die Positionen von Campern, die bereits ein Jahr alt sind, keinen Einfluss auf Ihre Analyse der diesjährigen Waldbrandherde haben. Die Einsicht in die zeitlichen Eigenschaften der Waldbrände und Camper hat wichtige Auswirkungen auf die Zuteilung der Ressourcen für die Brandbekämpfung.
Interpretieren von Ergebnissen
Wenn das Werkzeug Kolokalitätsanalyse ausgeführt wird, fügt es den resultierenden Ausgabe-Features sechs Felder hinzu. Das Feld Local Colocation Quotient enthält den resultierenden Quotienten für jedes relevante Eingabe-Feature. Zudem wird der p-value angegeben. Die Quotienten für die lokale Kolokalität werden nach dem LCLQ Type des Features unterteilt (LCLQ Bin), beschriftet (LCLQ Type) und auf der Karte angezeigt. Features der Interessenskategorie (Kategorie A), die einen Quotienten für die lokale Kolokalität von mehr als 1 aufweisen, haben mit größerer Wahrscheinlichkeit Features der Nachbarkategorie (Kategorie B) in ihrer Nachbarschaft. Für Features mit Kolokalitätsquotienten von weniger als 1 ist die Wahrscheinlichkeit von Kategorie B in der Nachbarschaft weniger wahrscheinlich. Wenn ein Feature einen Kolokalitätsquotienten von 1 hat, bedeutet dies, dass das Verhältnis von Kategorien in der Nachbarschaft eine gute Repräsentation des Verhältnisses von Kategorien im gesamten Untersuchungsgebiet ist.
| Symbol | LCLQ-Bin | LCLQ-Typ | Beschreibung |
|---|---|---|---|
 | 0 | Kolokalität: Signifikant | Der Quotient für die lokale Kolokalität ist größer als 1, und der p-Wert ist kleiner als 0,05. |
 | 1 | Kolokalität: Nicht signifikant | Der Quotient für die lokale Kolokalität ist größer als 1, und der p-Wert ist größer als 0,05. |
 | 2 | Isolation: Signifikant | Der Quotient für die lokale Kolokalität ist gleich oder kleiner als 1, und der p-Wert ist kleiner als 0,05. |
 | 3 | Isolation: Nicht signifikant | Der Quotient für die lokale Kolokalität ist gleich oder kleiner als 1, und der p-Wert ist größer als 0,05. |
 | 4 | Undefiniert | In der Nachbarschaft des Features gibt es keine anderen Features, oder die Bandbreite ist gleich 0. |
Für die Nachbarschaft aller Features gibt das Feld Neighboring Categories alle Kategorien an, die in der angegebenen Nachbarschaft gefunden wurden. Im Feld Neighbor Prevalence wird erfasst, wie häufig beliebige Kombinationen von Nachbarkategorien in Nachbarschaften für die anderen relevanten Features vorkommen. Beispiel: Wenn Kategorie B als Nachbarkategorie vorkommt, ist Neighbor Prevalence von B gleich der Anzahl von Features, für die B als Nachbarkategorie vorkommt, geteilt durch die Gesamtzahl der relevanten Eingabe-Features. Dies kann nützlich sein, um zu erkunden, wie verbreitet diese Kombination (oder eine Teilmenge der Kombination) von Kategorien in Ihrem Untersuchungsgebiet ist. In der folgenden Tabelle ist dargestellt, dass Kategorie A in 100 % der Nachbarschaften vorkommt, eine Kombination von A und C dagegen nur in 20 % der Nachbarschaften:
| Kombinationen von Nachbarschaftskategorien | Verbreitung von Nachbarn |
|---|---|
A | 1 |
A | 1 |
A, B | 0,4 |
A, B | 0,4 |
A, C | 0,2 |
Zudem wird ein Scatterplot erstellt und kann unter Ausgabe-Features im Bereich Inhalt abgerufen werden. Er zeigt die Beziehung zwischen den Quotienten für die lokale Kolokalität und den berechneten p-Werten an. 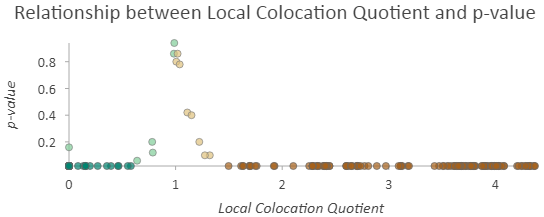
Zusätzliche Ressourcen
- Timothy F. Leslie, & Barry J. Kronenfeld (2011). "The Colocation Quotient: A New Measure of Spatial Association Between Categorical Subsets of Points." Geographical Analysis43 (3), 306-326. DOI: 10.1111/j.1538-4632.2011.00821.x
- Fahui Wang, Yujie Hu, Shuai Wang & Xiaojuan Li (2017). "Local Indicator of Colocation Quotient with a Statistical Significance Test: Examining Spatial Association of Crime and Facilities." The Professional Geographer69 (1), 22-31. DOI: 10.1080/00330124.2016.1157498