Mit der Spatial Analyst-Lizenz verfügbar.
Mit der 3D Analyst-Lizenz verfügbar.
Mit dem Werkzeug wird die Neigungsrichtung des Gefälles bestimmt. Die Werte der einzelnen Zellen im Ausgabe-Raster geben die Kompassrichtung an, der die Oberfläche an dieser Position zugewandt ist. Sie wird im Uhrzeigersinn in Grad von 0 (genau Norden) bis 360 (wieder genau Norden) im Vollkreis gemessen. Flache Bereiche ohne Neigungsrichtung erhalten den Wert -1.
Die folgenden Abbildungen zeigen ein Eingabe-Höhen-Dataset und das Ausgabe-Ausrichtungs-Raster.

Hinweis:
Das Werkzeug bietet eine neuere Implementierung der Ausrichtung und sollte statt des Werkzeugs Ausrichtung verwendet werden. Das Werkzeug Ausrichtung passt eine Ebene an die neun lokalen Zellen an. Allerdings ist eine Ebene möglicherweise kein guter Deskriptor der Landschaft, sodass relevante natürliche Variationen maskiert oder überhöht werden können. Das Werkzeug Oberflächenparameter passt eine Oberfläche an die benachbarten Zellen an, nicht an eine Ebene. Dadurch ermöglicht es eine natürlichere Anpassung an das Terrain.
Das Werkzeug Ausrichtung verwendet ein Fenster aus 3 mal 3 Zellen, um den Wert zu berechnen. Im Werkzeug Oberflächenparameter sind dagegen Fenstergrößen von 3 mal 3 bis 15 mal 15 Zellen möglich. Größere Fenster sind für Höhendaten mit hoher Auflösung nützlich, um Prozesse der Landoberfläche mit einem geeigneten Maßstab zu erfassen. Oberflächenparameter bietet zudem eine anpassungsfähige Fensteroption, die die lokale Variabilität des Terrains bewertet und die größte geeignete Nachbarschaftsgröße für jede Zelle identifiziert. Dies kann bei einem graduell homogenen Terrain, dass von Wasserläufen, Straßen oder tiefen Einschnitten in der Neigung unterbrochen ist, nützlich sein.
Sie können weiterhin dem traditionellen Ansatz des Werkzeugs Ausrichtung folgen, wenn die Ergebnisse genau mit früheren Ausführungen des Werkzeugs übereinstimmen müssen oder wenn eine schnelle Ausführung wichtiger als ein besserer Algorithmus ist.
Mit dem Werkzeug können Sie folgende Aktionen ausführen:
- Ermitteln aller nach Norden weisenden Neigungen eines Berges bei der Suche nach den besten Hängen für Skipisten
- Berechnen der Sonnenausleuchtung einzelner Orte in einer Region im Rahmen einer Studie zur Bestimmung der Artenvielfalt an den verschiedenen Orten
- Ermitteln aller Südhänge in einer gebirgigen Region, um die Orte ermitteln zu können, an denen Schnee zuerst schmilzt, und somit im Rahmen einer Studie die Wohngebiete zu identifizieren, in denen abfließendes Wasser zuerst durchkommt
- Ermitteln von flachem Land bei der Suche nach einer Fläche, auf der ein Flugzeug notlanden kann
Berechnungsmethoden und Kanteneffekt
Für die Berechnung der Ausrichtung stehen zwei Methoden zur Verfügung. Mit dem Parameter Methode können Sie zwischen der planaren oder der geodätischen Berechnung auswählen.
Bei der Methode "Planar" erfolgt die Berechnung in einer projizierten flachen Ebene mit einem kartesische Koordinatensysteme in 2D. Bei der geodätischen Methode erfolgt die Berechnung in einem kartesischen Koordinatensystems in 3D unter Berücksichtigung der Form der Erde als Ellipsoid.
Sowohl planare als auch geodätische Berechnungen werden anhand einer aus 3x3 Zellen bestehenden Zellengruppe (bewegliches Fenster) durchgeführt. Wenn die bearbeitete (mittlere) Zelle NoData ist, lautet die Ausgabe für jede Zellengruppe ebenfalls NoData. Zur Berechnung müssen außerdem mindestens sieben Zellen, die an die bearbeitete Zelle angrenzen, gültige Werte aufweisen. Sind weniger als sieben gültige Zellen vorhanden, erfolgt keine Berechnung, und die Ausgabe dieser zu verarbeitenden Zelle lautet "NoData".
Die Zellen der ganz am Rand des Ausgabe-Rasters befindlichen Zeilen und Spalten lauten "NoData". Das liegt daran, dass die Zellen entlang der Grenze des Eingabe-Datasets nicht an ausreichend viele andere Zellen angrenzen.
Methode "Planar"
Die Methode "Planar" ist die herkömmliche Methode zur Berechnung der Ausrichtung.
Algorithmus der planaren Ausrichtung
Ein sich bewegendes 3x3-Fenster durchläuft jede Zelle im Eingabe-Raster. Für jede Zelle in der Mitte des Fensters werden ein Ausrichtungs- und ein Neigungswert anhand eines Algorithmus berechnet, der die Werte der acht angrenzenden Zellen mit berücksichtigt. Die Zellen werden als Buchstaben a bis i identifiziert, wobei e die Zelle darstellt, für die die Ausrichtung berechnet wird.

Die Änderungsrate in der x-Richtung für Zelle e wird mit dem folgenden Algorithmus berechnet:
[dz/dx] = ((c + 2f + i)*4/wght1 – (a + 2d + g)*4/wght2) / 8- Dabei gilt:
wght1 und wght2 bezeichnen die horizontal gewichtete Anzahl der gültigen Zellen.
Beispiel:
- wenn c , f und i alle gültige Werte enthalten, wght1 = (1+2*1+1) = 4.
- wenn i NoData ist, wght1 = (1+2*1+0) = 3.
- wenn f NoData ist, wght1 = (1+2*0+1) = 2.
Die gleiche Logik gilt für wght2, nur dass die angrenzenden Positionen als a, d und g bezeichnet werden.
Die Änderungsrate in der y-Richtung für die Zelle e wird mit dem folgenden Algorithmus berechnet:
[dz/dy] = ((g + 2h + i)*4/wght3 – (a + 2b + c)*4/wght4 ) / 8- Dabei gilt:
wght3 und wght4 unterliegen denselben Prinzipien wie die Berechnung [dz/dx].
Unter Bezug auf die Änderungsrate in der x- und y-Richtung für Zelle e wird die Ausrichtung mit folgenden Werten berechnet:
aspect = 57,29578 * atan2 ([dz/dy], –[dz/dx])Der Ausrichtungswert wird dann in Kompassausrichtungswerte (0-360 Grad) konvertiert. Dabei gilt die folgende Regel:
if aspect < 0 cell = 90.0 - aspect> else if aspect > 90.0 cell = 360.0 - aspect + 90.0 else cell = 90.0 - aspectBeispiel für eine planare Ausrichtungsberechnung
Ein Beispiel: Der Ausrichtungswert der mittleren Zelle des sich bewegenden Fensters wird berechnet.

Die Änderungsrate in der x-Richtung für die mittlere Zelle e lautet:
[dz/dx] = ((c + 2f + i)*4/wght1 – (a + 2d + g)*4/wght2) / 8 = ((85 + 170 + 84)*4/(1+2+1) – (101 + 202 + 101)*4/(1+2+1)) / 8 = –8,125Die Änderungsrate in der y-Richtung für die Zelle e lautet:
[dz/dy] = ((g + 2h + i)*4/wght3 – (a + 2b + c)*4/wght4) / 8 = ((101 + 182 + 84)*4/(1+2+1) – (101 + 184 + 85)*4/(1+2+1)) / 8 = –0,375Die Ausrichtung wird wie folgt berechnet:
aspect = 57,29578 * atan2 ([dz/dy], –[dz/dx]) = 57,29578 * atan2 (–0,375, 8,125) = –2,64Da der berechnete Wert kleiner als 0 ist, wird die letzte Regel folgendermaßen angewendet:
cell = 90,0 – aspect = 90 – (–2,64) = 90 + 2,64 = 92,64Der Wert 92.64 für die mittlere Zelle e bedeutet, dass die Ausrichtung in östlicher Richtung liegt.

Geodätische Methode
Bei der geodätischen Methode wird die Oberflächenausrichtung in einem geozentrischen 3D-Koordinatensystem gemessen, das auch als ECEF-Koordinatensystem (Earth Centered, Earth Fixed) bezeichnet wird, indem die Form der Erde als Ellipsoid berücksichtigt wird. Das Ergebnis der Berechnung hat keine Auswirkungen auf die Projektion des Datasets. Es werden die Z-Einheiten des Eingabe-Rasters verwendet, wenn sie im Raumbezug definiert sind. Wenn keine Z-Einheiten im Raumbezug der Ausgabe definiert sind, müssen diese mit dem Z-Einheitenparameter definiert werden. Bei der geodätischen Methode ist die Berechnung der Ausrichtung genauer als bei der planaren Methode.
Transformation geodätischer Koordinaten
Das ECEF-Koordinatensystem ist ein nach rechts ausgerichtetes kartesisches 3D-Koordinatensystem mit dem Erdmittelpunkt als Ursprung, in dem jede Position durch X-, Y- und Z-Koordinaten dargestellt wird. In der nachfolgenden Abbildung sehen Sie ein Beispiel für eine Zielposition T, die durch geozentrische Koordinaten ausgedrückt wird.
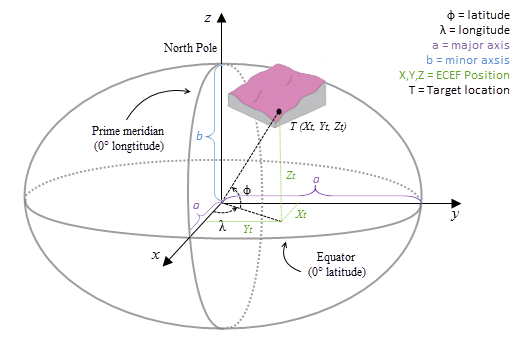
Die geodätische Berechnung verwendet eine X-, Y-, Z-Koordinate, die basierend auf ihrer geodätischen Koordinaten (Breitengrad φ, Längengrad λ, Höhe h) berechnet wird. Wenn das Koordinatensystem des Eingabe-Oberflächen-Rasters ein projiziertes Koordinatensystem (PCS) ist, wird das Raster zunächst erneut in ein geographisches Koordinatensystem (GCS) projiziert, wo jede Position eine geodätische Koordinate aufweist, und wird dann in das ECEF-Koordinatensystem transformiert. Die Höhe (Z-Wert) ist die Ellipsoidhöhe, die auf die Ellipsoidoberfläche referenziert wird. Weitere Informationen können der Grafik in der Abbildung unten entnommen werden.
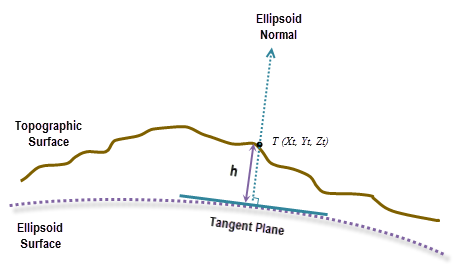
Verwenden Sie die folgenden Formeln, um geodätische Koordinaten (Breitengrad φ, Längengrad λ, Höhe h) in ECEF-Koordinaten zu transformieren:
X = (N(φ)+h)cosφcosλY = (N(φ)+h)cosφsinλZ = (b2/a2*N(φ)+h)sinφ- Dabei gilt:
- N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
- φ = Breitengrad
- λ = Längengrad
- h = Ellipsoidhöhe
- a = Hauptachse des Ellipsoids
- b = Nebenachse des Ellipsoids
In den oben aufgeführten Formeln ist die Ellipsoidhöhe h in Meter angegeben. Wenn die Z-Einheit Ihres Eingabe-Raster in einer anderen Einheit vorliegt, wird sie intern in Meter transformiert.
Berechnung der Ausrichtung
Die geodätische Ausrichtung an einer Position ist die Richtung der Neigungsoberfläche in Bezug auf Norden auf einer Ebene parallel zur ellipsoiden Oberfläche.
Um die Ausrichtung an den einzelnen Positionen zu berechnen, wird eine aus 3 x 3 Zellen bestehende Zellengruppe um jede bearbeitete Zelle per LSM (Least Squares Method) angepasst. Die beste Anpassung der LSM minimiert die Summe der quadrierten Differenz (dzi) zwischen dem tatsächlichen und dem angepassten Z-Wert. Ein Beispiel finden Sie in der Abbildung unten.

Hier ist die Ebene als z = Ax + By + C dargestellt. Für jeden Zellenmittelpunkt ist dzi die Differenz zwischen dem tatsächlichen und dem angepassten Z-Wert.
Die Ebene wird optimal angepasst, wenn ∑9i=1dzi2 minimiert wird.
Nachdem die Ebene angepasst wurde, wird eine Oberflächennormale an der Zellenposition berechnet. An derselben Position wird ebenfalls eine Ellipsoidnormale rechtwinklig zur Tangentenebene der Ellipsoidoberfläche berechnet.
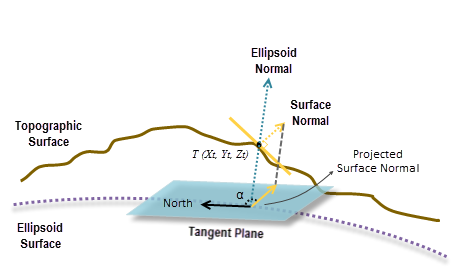
Da die Tangentenebene der Ellipsoid-Oberfläche als Referenzebene betrachtet wird, ist die Oberflächennormale rechtwinklig zur Ebene. Letztlich wird die geodätische Ausrichtung durch Messen des Winkels α im Uhrzeigersinn zwischen Norden und der rechtwinkligen Projektion der Oberflächennormale berechnet (siehe Abbildung unten).
Sollte ich das Werkzeug "Oberflächenparameter" verwenden?
Wenn der Wert des Parameters Eingabe-Raster (in_raster in Python) eine hohe Auflösung für eine geringere Zellengröße als einige Meter angibt oder besonders verrauscht ist, sollten Sie das Werkzeug Oberflächenparameter und seine Option für die benutzerdefinierte Nachbarschaftsentfernung statt seiner Option für die unmittelbare 3-mal-3-Nachbarschaft verwenden. Die Auswirkung verrauschter Oberflächen kann durch Verwendung einer größeren Nachbarschaft minimiert werden. Mit einer größeren Nachbarschaft lassen sich auch Terrains und Oberflächeneigenschaften besser darstellen, wenn Oberflächen mit hoher Auflösung verwendet werden.
Verwendung einer GPU
Für die geodätische Methode kann mit diesem Werkzeug die Performance gesteigert werden, wenn Sie eine bestimmte GPU-Hardware auf Ihrem System installiert haben. Weitere Informationen zur Unterstützung, Konfiguration und Aktivierung dieser Funktion finden Sie unter GPU-Verarbeitung mit Spatial Analyst.
Referenzen
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Bd. 60, Nr. 2, 2011, S. 145-159
E.J.Krakiwsky, and D.E.Wells, 1971. Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, No16, 1971, S. 18–38
Lancaster, P. und Šalkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS – theory and practice Abschnitt 10.2.1. S. 282.
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), S. 3.