Quantil-Quantil-Plots (Q-Q-Plots) sind ein exploratives Werkzeug zum Untersuchen der Ähnlichkeit zwischen der Verteilung einer numerischen Variable und einer Normalverteilung oder zwischen den Verteilungen von zwei numerischen Variablen.
Es gibt zwei Typen von Q-Q-Plots: Q-Q-Plots für normalverteilte Daten und allgemeine Q-Q-Plots.
- In Q-Q-Plots für normalverteilte Daten werden die Quantile einer numerischen Variable den Quantilen einer Normalverteilung gegenübergestellt.
- In allgemeinen Q-Q-Plots werden die Quantile der einen numerischen Variable den Quantilen einer zweiten numerischen Variable gegenübergestellt.
Wenn die Verteilungen der verglichenen Quantile identisch sind, bilden die dargestellten Punkte eine 45-Grad-Gerade. Je weiter die dargestellten Punkte von einer Geraden abweichen, desto weniger ähnlich sind die verglichenen Verteilungen.
Variablen
Für Q-Q-Plots für normalverteilte Daten ist eine numerische Variable erforderlich, die einer Normalverteilung gegenübergestellt wird. Für allgemeine Q-Q-Plots sind zwei numerische Variablen erforderlich, die einander gegenübergestellt werden.
Transformation
Einige analytische Methoden erfordern, dass die Daten normal verteilt sind. Wenn die Daten verzerrt sind (die Verteilung ist einseitig schief), sollten Sie die Daten transformieren, um eine Normalverteilung herzustellen. Mit Q-Q-Plots für normalverteilte Daten können Sie die Effekte von logarithmischen und Quadratwurzel-Transformationen auf die Verteilung Ihrer Daten beim Vergleich mit einer Normalverteilung erkunden.
Logarithmische Transformation
Die logarithmische Transformation wird häufig dann verwendet, wenn die Daten eine positiv verzerrte Verteilung haben und nur wenige große Werte vorhanden sind. Wenn diese großen Werte in Ihrem Dataset vorhanden sind, hilft die logarithmische Transformation, konstantere Varianzen zu erreichen und Ihre Daten zu normalisieren.
Hinweis:
Logarithmische Transformationen können nur dann angewendet werden, wenn alle Werte der Variablen größer als Null sind. Null-Werte führen zu einem Fehler.
Quadratwurzel-Transformation
Eine Quadratwurzel-Transformation ähnelt einer logarithmischen Transformation dadurch, dass sie die rechtsseitige Schiefe eines Datasets verringert. Im Gegensatz zur logarithmischen Transformation kann die Quadratwurzel-Transformation auch auf die Null angewendet werden.
Hinweis:
Quadratwurzel-Transformationen können nur dann angewendet werden, wenn alle Werte der Variablen größer als oder gleich Null sind. Negative Werte führen zu einem Fehler.
Invers
Bei einer Kehrwerttransformation wird der reziproke Wert (1/x) der einzelnen Werte (x) in dem Feld verwendet.
Hinweis:
Kehrwerttransformationen können nicht auf Null-Werte angewendet werden. Null-Werte in dem Feld werden als NULL-Werte behandelt.
Box-Cox
Bei einer Box-Cox-Transformation wird die folgende Potenzfunktion auf normal verteilte Werte angewendet:
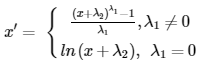
Hinweis:
Box-Cox-Transformationen können nur auf positive Werte angewendet werden. In Fällen, in denen negative oder Null-Werte vorhanden sind, verwenden Sie den Versatzparameter, um sicherzustellen, dass alle Werte positiv sind.
Achsen
Achsengrenzen
Die Standardgrenzen für das Minimum und das Maximum der Achsen werden entsprechend dem Bereich der Datenwerte auf der Achse festgelegt. Diese Werte können durch Eingabe eines neuen gewünschten Wertes für die Achsengrenze angepasst werden. Durch Klicken auf das Symbol "Zurücksetzen" wird die Achsengrenze wieder auf den Standardwert zurückgesetzt.
Zahlenformat
Sie können formatieren, wie auf einer Achse numerische Werte dargestellt werden, indem Sie eine Zahlenformatkategorie angeben oder eine benutzerdefinierte Formatzeichenfolge definieren.
Aussehen
Titel und Beschreibung
Diagramme und Achsen erhalten Standardtitel basierend auf den Variablennamen und dem Diagrammtyp. Diese können auf der Registerkarte Allgemein im Bereich Diagrammeigenschaften bearbeitet werden. Sie können auch eine Beschreibung für das Diagramm eingeben, wobei es sich um einen Textblock handelt, der am unteren Rand des Diagrammfensters angezeigt wird.
Farbe
Q-Q-Plots übernehmen ihre Umrisslinie und Füllfarben aus der Symbolisierung des Quell-Layers. Wenn ein Layer mit einem anderen Attribut als einer der Q-Q-Plot-Variablen symbolisiert wird, kann eine dritte Variable in der Visualisierung des Q-Q-Plots angezeigt werden.
Führungslinien
Führungslinien oder Bereiche können als Referenz oder zum Hervorheben signifikanter Werte zu Diagrammen hinzugefügt werden. Um eine neue Führungslinie zur Registerkarte Führungslinien im Bereich Diagrammeigenschaften hinzuzufügen, klicken Sie auf Führungslinie hinzufügen. Um eine Linie zu zeichnen, geben Sie einen Wert ein, wo die Linie gezeichnet werden soll. Um einen Bereich zu erstellen, geben Sie einen Wert bis ein. Sie können optional Text zur Führungslinie hinzufügen, indem Sie Beschriftung angeben.
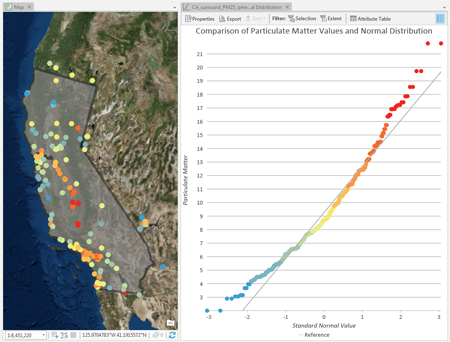
Beispiel
Erstellen eines Q-Q-Plots zum Untersuchen, ob bestimmte Materialproben in Kalifornien normal verteilt sind.
- Die Verteilung vergleichen von:Particulate Matter
- Mit Transformation: Keine
- Mit: <Normalverteilung>